Question

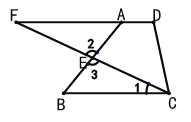
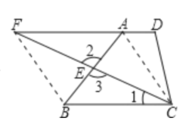
【题目】已知：如图，在梯形 ABCD 中，AD∥BC，E 是 AB 的中点，CE 的延长线与 DA 的延长线相 交于点 F．

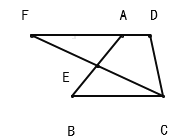
（1）求证：△BCE≌△AFE；

（2）连接 AC、FB，则 AC 与 FB 的数量关系是 ，位置关系是 ．

Answer 1

【答案】（1）见解析；（2）相等， 平行

【解析】

（1）根据平行线的性质推出∠1=∠F，根据线段的中点的定义和对顶角性质得出BE=AE，∠3=∠2，根据AAS即可证出答案.

（2）由（1）知：△BCE≌△AFE，推出CE=FE，AE=BE，根据平行四边形的判定即可得到平行四边形AFBC，即可得出答案．

（1）∵AD∥BC，

∴∠1 ＝∠F．

∵点 E 是 AB 的中点，

∴BE＝AE.

在△BCE 和△AFE 中，

∴△BCE≌△AFE（AAS）.

（2）由（1）已知：△BCE≌△AFE

∴CE=FE

∵AE=BE

∴四边形AFBC是平行四边形

∴AC∥BF，AC=BF

故答案为：相等，平行.