题目内容
【题目】如图,已知∠AOB=90°,射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转;同时,射线OD绕点O从OB位置开始,以每秒1°的速度逆时针方向旋转.当OC与OA成180°时,OC与OD同时停止旋转.

(1)当OC旋转10秒时,∠COD= °.
(2)当旋转时间为 秒时,OC与OD的夹角是30°.
(3)当旋转时间为 秒时,OB平分∠COD时.
【答案】(1)∠COD=40°;(2)12或24;(3)30.
【解析】试题分析:(1)根据旋转的速度和旋转的时间分别求出∠AOC和∠BOD的度数,然后根据∠COD=∠AOB-∠AOC-∠BOD即可计算得出结论;
(2)设转动t秒,OC与OD的夹角是30度,①如图1,列方程即可得到结论;②如图2,列方程即可得到结论;
(3)如图3,设转动m秒时,根据角平分线的定义列方程即可得到结论.
试题解析:
解:(1)∵射线OC绕点O从OA位置开始,以每秒4°的速度顺时针方向旋转,
∴当OC旋转10秒时,∠COD=∠AOB-4°×10-1°×10=40°,
故答案为:40;
(2)设转动t秒,OC与OD的夹角是30度,
①如图1,4t+t=90-30,

t=12,
②如图2,4t+t=90+30,

t=24,
∴旋转的时间是12秒或24秒,
故答案为12或24;
(3)如图3,设转动m秒时,OB平分∠COD,
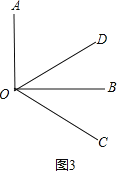
则4m-90=m,
解得,m=30,
∴旋转的时间是30秒,
故答案为30.

练习册系列答案
相关题目