Question

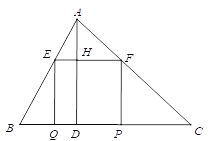
【题目】如图，已知矩形EFPQ的一边QP在BC边上，E、F两点分别在AB、AC上，AD是BC边上的高，AD交EF于H．

（1）求证： ；

（2）若BC=10，高AD=8，设EF=x，矩形EFPQ的面积为y，求y与x的函数关系式，并求y的最大值；

（3）若BC=a，高AD=b，直接写出矩形EFPQ的面积的最大值___________．（用a，b表示）

Answer 1

【答案】（1）见解析；（2）y=，20；（3）．

【解析】（1）由EF∥BC，得到△AEF∽△ABC，由相似三角形对应高之比等于相似比即可得到结论；

（2）由（1）的结论，求出AH、HD的长，由EFPQ的面积=EF×HD即可得到结论；

（3）类似（2）可得到结论．

（1）∵四边形EFPQ是矩形，∴EF∥BC，∴△AEF∽△ABC，∴；

（2）由（1）得：，∴，∴AH=0.8x，∴HD=AD－AH=8-0.8x，∴y=EFPQ的面积=EF×HD=x（8-0.8x）=，∴当x=5时，y的最大值为20．

（3）∵，∴，∴AH=，∴矩形EFPQ的面积=EF×HD==，∴矩形EFPQ的面积的最大值为．