题目内容
已知线段AB和线段CD分别为一个梯形的两个底边,且BC⊥CD,AB=2√3,BC=3,S△BCD=
 ,则AD等于 。
,则AD等于 。

 ,则AD等于 。
,则AD等于 。2 或2
或2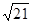
 或2
或2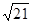
由且BC⊥CD,BC=3,S△BCD= 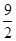
 ,求得CD等于3
,求得CD等于3 ,作AE⊥CD,在直角三角形ADE中利用勾股定理从而求得AD.
,作AE⊥CD,在直角三角形ADE中利用勾股定理从而求得AD.
解:图一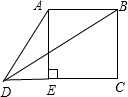
图二: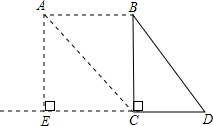
作AE⊥CD,连接BD
由图一
∵S△BCD=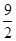
 ,BC⊥CD,
,BC⊥CD,
∴CD=3 ,
,
∵tg∠BDC= ,
,
∴∠BDC=30°,
∵在Rt△ADE中,AE=3,DE=3 -2
-2 =
= ,
,
∴AD= =2
=2 ,
,
由图二
延长BC,做AE⊥ED于点E.
由题意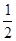 BC?CD=
BC?CD=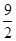
 ,
,
解得CD=3 ,
,
(CD+EC)2+AE2=AD2
(5 )2+9=AD2
)2+9=AD2
则AD=2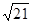 .
.
故答案为:2 或2
或2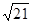 .
.
本题考查了把梯形问题运用到直角三角形中,利用勾股定理来解决问题.
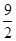
 ,求得CD等于3
,求得CD等于3 ,作AE⊥CD,在直角三角形ADE中利用勾股定理从而求得AD.
,作AE⊥CD,在直角三角形ADE中利用勾股定理从而求得AD.解:图一

图二:

作AE⊥CD,连接BD
由图一
∵S△BCD=
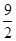
 ,BC⊥CD,
,BC⊥CD,∴CD=3
 ,
,∵tg∠BDC=
 ,
,∴∠BDC=30°,
∵在Rt△ADE中,AE=3,DE=3
 -2
-2 =
= ,
,∴AD=
 =2
=2 ,
,由图二
延长BC,做AE⊥ED于点E.
由题意
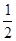 BC?CD=
BC?CD=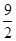
 ,
,解得CD=3
 ,
,(CD+EC)2+AE2=AD2
(5
 )2+9=AD2
)2+9=AD2则AD=2
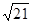 .
.故答案为:2
 或2
或2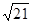 .
.本题考查了把梯形问题运用到直角三角形中,利用勾股定理来解决问题.

练习册系列答案
 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目

 ,则
,则
 ,则
,则



 中,点
中,点 是
是 的中点,连接
的中点,连接 、
、 ,点
,点 是
是 、
、 ,点
,点 是
是 ,过点
,过点 于点
于点 ,连接
,连接 .下列结论中
.下列结论中 ;②
;② ;③
;③ ;④
;④
