题目内容
如图，梯形ABCD中，AB∥CD，∠DAB＝90°，F是BC的中点，
连接DF并延长DF交AB于点E，连接AF。
小题1:（1）求证：△CDF≌△BEF；
小题2:（2）若∠E＝28°，求∠AFD的度数。
连接DF并延长DF交AB于点E，连接AF。
小题1:（1）求证：△CDF≌△BEF；
小题2:（2）若∠E＝28°，求∠AFD的度数。
小题1:（1）证明：如图1，∵AB∥CD，F是BC的中点
∴∠C＝∠3，CF＝FB
又∵∠1＝∠2
∴△CDF≌△BEF（ASA
小题2:（2）由（1）可知，∠E＝∠CDF＝28°
∵∠ADC＝∠DAB＝90°
∴∠ADF＝90°－28°＝62°
在Rt△DAE中，F为斜边中点
∴AF＝FD
∴∠FDA＝∠FAD＝62°
∴∠AFD＝180°－62°－62°＝56°
略
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
的两条对角线相交于点
，
，
，
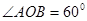平分
交
于点
.则
的长为 ,
的长为 ．
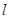上有三个正方形
，若
的面积分别为6和12，则
的面积为_________.
，则AD等于 。
，
，B点坐标为(4,0).点
是边
上一点,且
.点
、
分别从
、
同时出发，以1厘米/秒的速度分别沿
、
向点
运动（当点F运动到点B时，点E随之停止运动），EM、CD的延长线交于点P，FP交AD于点Q.⊙E半径为
，设运动时间为
秒。
？
等于（ ）
