题目内容
【题目】如图,CD为⊙O的直径,CD⊥AB,垂足为点F,AO⊥BC,垂足为点E,AO=1.

(1)求∠C的大小;
(2)求阴影部分的面积.
【答案】解:(1)∵CD是圆O的直径,CD⊥AB,∴![]() 。∴∠C=
。∴∠C=![]() ∠AOD。
∠AOD。
∵∠AOD=∠COE,∴∠C=![]() ∠COE。
∠COE。
∵AO⊥BC,∴∠C=30°。
(2)连接OB,
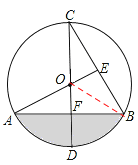
由(1)知,∠C=30°,∴∠AOD=60°。∴∠AOB=120°。
在Rt△AOF中,AO=1,∠AOF=60°,∴AF=![]() ,OF=
,OF=![]() 。
。
∴AB=![]() 。
。
∴![]() 。
。
【解析】试题分析:(1)根据垂径定理可得![]() =
=![]() ,∠C=
,∠C=![]() ∠AOD,然后在Rt△COE中可求出∠C的度数.
∠AOD,然后在Rt△COE中可求出∠C的度数.
(2)连接OB,根据(1)可求出∠AOB=120°,在Rt△AOF中,求出AF,OF,然后根据S阴影=S扇形OAB﹣S△OAB,即可得出答案.
解:(1)∵CD是圆O的直径,CD⊥AB,
∴![]() =
=![]() ,
,
∴∠C=![]() ∠AOD,
∠AOD,
∵∠AOD=∠COE,
∴∠C=![]() ∠COE,
∠COE,
∵AO⊥BC,
∴∠C=30°.
(2)连接OB,
由(1)知,∠C=30°,
∴∠AOD=60°,
∴∠AOB=120°,
在Rt△AOF中,AO=1,∠AOF=60°,
∴AF=![]() ,OF=
,OF=![]() ,
,
∴AB=![]() ,
,
∴S阴影=S扇形OADB﹣S△OAB=![]() ﹣
﹣![]() ×
×![]() ×
×![]() =
=![]() π﹣
π﹣![]() .
.

练习册系列答案
相关题目