题目内容
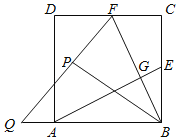
【题目】如图,正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论①AE=BF;②AE⊥BF;③S四边形ECFG=2S△BGE.正确的有_____.(填正确结论的序号)
【答案】①②
【解析】
先证明△ABE≌△BCF,再利用角的关系求得∠BGE=90°,即可得到①AE=BF;②AE⊥BF;根据AA可证△BGE与△BCF相似,进一步得到相似比,再根据相似三角形的性质即可求解.
解:∵E,F分别是正方形ABCD边BC,CD的中点,
∴CF=BE,
在△ABE和△BCF中,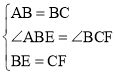 ,
,
∴Rt△ABE≌Rt△BCF(SAS),
∴∠BAE=∠CBF,AE=BF,故①正确;
又∵∠BAE+∠BEA=90°,
∴∠CBF+∠BEA=90°,
∴∠BGE=90°,
∴AE⊥BF,故②正确;
∵∠BGE=∠BCF,∠GBE=∠CBF,
∴△BGE∽△BCF,
∵BE=![]() BC,BF=
BC,BF=![]() BC,
BC,
∴BE:BF=1:![]() ,
,
∴△BGE的面积:△BCF的面积=1:5,
∴S四边形ECFG=4S△BGE,故③错误.
故答案为:①②.

练习册系列答案
相关题目
【题目】某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 11 | 15 | 23 | 28 | 18 | 5 |
(1)这天部分出行学生使用共享单车次数的中位数是 ,众数是 .
(2)这天部分出行学生平均每人使用共享单车约多少次?(结果保留整数)
(3)若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.