题目内容
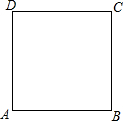如图所示，在边长为4的正方形ABCD的边上有一个动点P，从点B出发，沿BC运动到点C，设点P（不与B、C重合）运动的路程为x，梯形APCD的面积为y，则y与x之间的函数关系式是16-2x
16-2x
，其中自变量x的取值范围是0＜x＜4
0＜x＜4
．分析：四边形APCD的面积=□ABCD的面积-△ABP的面积，有了正方形的边长和BP的长，就能表示出正方形和△ABP的面积，进而可得出y与x的函数关系式．由于P从B运动到C，所以自变量的取值范围应该在0-4之间．
解答：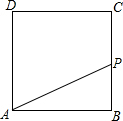
解：∵S四边形APCD=S□ABCD-S△ABP，
∴y=16-
x×4=16-2x（0＜x＜4）；
故答案是：16-2x．
解：∵S四边形APCD=S□ABCD-S△ABP，∴y=16-
| 1 |
| 2 |
故答案是：16-2x．
点评：本题考查了一次函数与一元一次方程的应用，解题的关键是列出函数关系式．
练习册系列答案
中考解读考点精练系列答案
相关题目
如图所示，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（ ）
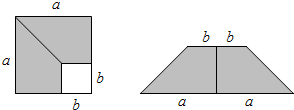
| A、（a-b）2=a2-2ab+b2 | B、（a+b）2=a2+2ab+b2 | C、a2-b2=（a+b）（a-b） | D、a2+ab=a（a+b） |
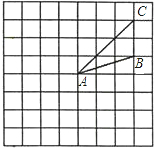如图所示，在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′，并计算对应点B和B′之间的距离．
如图所示，在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°，再向下平移2格后的图形△A′B′C′．