题目内容
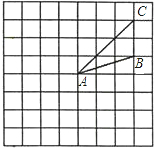如图所示，在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′，并计算对应点B和B′之间的距离．
分析：在AB的左边做AB′⊥AB，AC′⊥AC，且AB′=AB，AC′=AC，连接B′C′即可；把BB′放在直角边长为2，4的直角三角形的斜边上，利用勾股定理即可求得BB′长．
解答：解：所画图形如下所示：
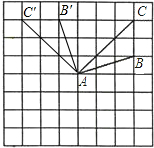
△A′B′C′即为所求；
其中B和B¹之间的距离为
=2
．
△A′B′C′即为所求；
其中B和B¹之间的距离为
| 22+42 |
| 5 |
点评：本题考查旋转作图及勾股定理的灵活运用．要注意旋转的三要素：①定点-旋转中心；②旋转方向；③旋转角度．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在边长为a的正方形中，剪去一个边长为b的小正方形（a＞b），将余下部分拼成一个梯形，根据两个图形阴影部分面积的关系，可以得到一个关于a、b的恒等式为（ ）
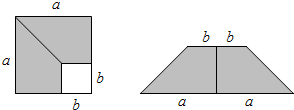
| A、（a-b）2=a2-2ab+b2 | B、（a+b）2=a2+2ab+b2 | C、a2-b2=（a+b）（a-b） | D、a2+ab=a（a+b） |
如图所示，在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°，再向下平移2格后的图形△A′B′C′．