题目内容
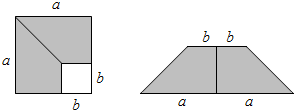
如图所示,在边长为a的正方形中,剪去一个边长为b的小正方形(a>b),将余下部分拼成一个梯形,根据两个图形阴影部分面积的关系,可以得到一个关于a、b的恒等式为( )

| A、(a-b)2=a2-2ab+b2 | B、(a+b)2=a2+2ab+b2 | C、a2-b2=(a+b)(a-b) | D、a2+ab=a(a+b) |
分析:可分别在正方形和梯形中表示出阴影部分的面积,两式联立即可得到关于a、b的恒等式.
解答:解:正方形中,S阴影=a2-b2;
梯形中,S阴影=
(2a+2b)(a-b)=(a+b)(a-b);
故所得恒等式为:a2-b2=(a+b)(a-b).
故选:C.
梯形中,S阴影=
| 1 |
| 2 |
故所得恒等式为:a2-b2=(a+b)(a-b).
故选:C.
点评:此题主要考查的是平方差公式的几何表示,运用不同方法表示阴影部分面积是解题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
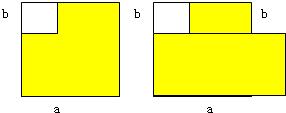
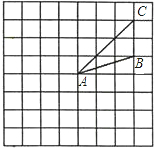 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°后的图形△A′B′C′,并计算对应点B和B′之间的距离.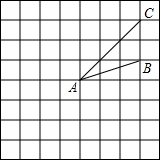 如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.
如图所示,在边长为1的网格中作出△ABC绕点A按逆时针方向旋转90°,再向下平移2格后的图形△A′B′C′.