题目内容
在平面直角坐标系XOY中,直线l1过点A(1,0)且与y轴平行,直线l2过点B(0,2)且与x轴平行,直线l1与直线l2相交于点P.点E为直线l2上一点,反比例函数y=![]() (k>0)的图象过点E与直线l1相交于点F.
(k>0)的图象过点E与直线l1相交于点F.
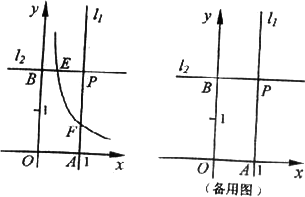
(1)若点E与点P重合,求k的值;
(2)连接OE、OF、EF.若k>2,且△OEF的面积为△PEF的面积的2倍,求E点的坐标;
(3)是否存在点E及y轴上的点M,使得以点M、E、F为顶点的三角形与△PEF全等?若存在,求E点坐标;若不存在,请说明理由.
解析:
|
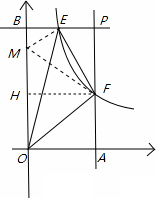
解:(1)若点E与点D重合,则k=1×2=2; (2)当k>2时,如图,点E、F分别在P点的右侧和上方,过E作x轴的垂线EC,垂足为C,过F作y轴的垂线FD,垂足为D,EC和FD相交于点G,则四边形OCGD为矩形,
∵PF⊥PE, ∴S△FPE= ∴四边形PFGE是矩形, ∴S△PFE=S△GEF, ∴S△OEF=S矩形OCGD-S△DOF-S△EGD-S△OCE= ∵S△OEF=2S△PEF, ∴ 解得k=6或k=2, ∵k=2时,E、F重合, ∴k=6, ∴E点坐标为:(3,2); (3)存在点E及y轴上的点M,使得△MEF≌△PEF, ①当k<2时,如图,只可能是△MEF≌△PEF,作FH⊥y轴于H,
分析:(1)根据反比例函数中k=xy进行解答即可; (2)当k>2时,点E、F分别在P点的右侧和上方,过E作x轴的垂线EC,垂足为C,过F作y轴的垂线FD,垂足为D,EC和FD相交于点G,则四边形OCGD为矩形,再求出S△FPE= (3)①当k<2时,只可能是△MEF≌△PEF,作FH⊥y轴于H,由△FHM∽△MBE可求出BM的值,再在Rt△MBE中,由勾股定理得,EM2=EB2+MB2,求出k的值,进而可得出E点坐标; ②当k>2时,只可能是△MFE≌△PEF,作FQ⊥y轴于Q,△FQM∽△MBE得, 点评:本题考查的是相似三角形的判定与性质,涉及到反比例函数的性质、全等三角形的判定与性质及勾股定理,解答此题的关键是根据题意作出辅助线,构造出相似三角形,利用相似三角形的性质解答. |

 阅读快车系列答案
阅读快车系列答案



 如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点.
如图,在平面直角坐标系xOy中,△ABC的A、B两个顶点在x轴上,顶点C在y轴的负半轴上.已知|OA|:|OB|=1:5,|OB|=|OC|,△ABC的面积S△ABC=15,抛物线y=ax2+bx+c(a≠0)经过A、B、C三点. 如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为
如图,在平面直角坐标系xOy中,A(2,1)、B(4,1)、C(1,3).与△ABC与△ABD全等,则点D坐标为