题目内容
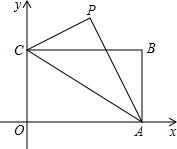
如图,矩形OABC的长OA=
,宽OC=1,将△AOC沿AC翻折得△APC,可得下列结论:①∠PCB=30°;②点P的坐标是(
,
);③若P、C两点在抛物线y=-
x2+bx+c上,则b的值是-
,c的值是1;④在③中的抛物线CP段(不包括C、P两点)上,存在一点Q,使四边形QCAP的面积最大,最大值为
.其中正确的有( )
| 3 |
| ||
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
9
| ||
| 16 |
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |

在Rt△OAC中,OA=
,OC=1,则∠OAC=30°,∠OCA=60°;
根据折叠的性质知:OA=AP=
,∠ACO=∠ACP=60°;
①∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°,故①正确;
②过P作PD⊥OA于D;
Rt△PAD中,∠PAD=60°,AP=
;
∴OD=AD=
,PD=
,
所以P(
,
),故②正确;
③将P、C代入抛物线的解析式中,得:
,
解得
;
故③错误;
④过Q作QM∥y轴,交CP于M;
由③知y=-
x2+
x+1,
由P(
,
),C(0,1)易求得直线PC:y=
x+1;
设M(a,
a+1),
则Q(a,-
a2+
a+1),则:
QM=-
a2+
a+1-(
a+1)=-
a2+
a,
故S△QPC=
QM•|xP|=
×(-
a2+
a)×
=-
a2+
a,
由于S△APC=S△AOC=
,
故四边形QCAP的面积S=S△QPC+S△APC=-
a2+
a+
,
则Smax=
=
;
故④正确;
所以正确的结论为①②④.
故选B.
| 3 |
根据折叠的性质知:OA=AP=
| 3 |
①∵∠BCA=∠OAC=30°,且∠ACP=60°,
∴∠PCB=30°,故①正确;
②过P作PD⊥OA于D;
Rt△PAD中,∠PAD=60°,AP=
| 3 |
∴OD=AD=
| ||
| 2 |
| 3 |
| 2 |
所以P(
| ||
| 2 |
| 3 |
| 2 |

③将P、C代入抛物线的解析式中,得:
|
解得
|
故③错误;
④过Q作QM∥y轴,交CP于M;
由③知y=-
| 4 |
| 3 |
| 3 |
由P(
| ||
| 2 |
| 3 |
| 2 |
| ||
| 3 |
设M(a,
| ||
| 3 |
则Q(a,-
| 4 |
| 3 |
| 3 |
QM=-
| 4 |
| 3 |
| 3 |
| ||
| 3 |
| 4 |
| 3 |
2
| ||
| 3 |
故S△QPC=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
2
| ||
| 3 |
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
由于S△APC=S△AOC=
| ||
| 2 |
故四边形QCAP的面积S=S△QPC+S△APC=-
| ||
| 3 |
| 1 |
| 2 |
| ||
| 2 |
则Smax=
4×(-
| ||||||||||
4×(-
|
9
| ||
| 16 |
故④正确;
所以正确的结论为①②④.
故选B.

练习册系列答案
相关题目



 ______m2、______m2,在这些数中,x取______m时,面积S最大.
______m2、______m2,在这些数中,x取______m时,面积S最大.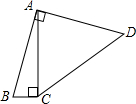
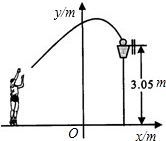 单位:m).请你根据所得的解析式,回答下列问题:
单位:m).请你根据所得的解析式,回答下列问题: