题目内容
如图,在矩形ABCD中,AB=6米,BC=8米,动点P以2米/秒的速度从点A出发,沿AC向点C移动,同时动点Q以1米/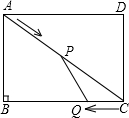 秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2.
秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2.
(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由.
 秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2.
秒的速度从点C出发,沿CB向点B移动,设P、Q两点移动t秒(0<t<5)后,四边形ABQP的面积为S米2.(1)求面积S与时间t的关系式;
(2)在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积能否相等?若能,求出此时点P的位置;若不能,请说明理由.
(1)过点P作PE⊥BC于E
Rt△ABC中,AC=
=
=10(米)
由题意知:AP=2t,CQ=t,则PC=10-2t
由AB⊥BC,PE⊥BC得PE∥AB
∴
=
即:
=
,
∴PE=
(10-2t)=-
t+6
又∵S△ABC=
×6×8=24
∴S=S△ABC-S△PCQ=24-
•t•(-
t+6)=
t2-3t+24
即:S=
t2-3t+24(8分)
(2)假设四边形ABQP与△CPQ的面积相等,则有:
t2-3t+24=12
即:t2-5t+20=0
∵b2-4ac=(-5)2-4×1×20<0
∴方程无实根
∴在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积不能相等.
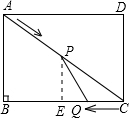
Rt△ABC中,AC=
| AB2+BC2 |
| 62+82 |
由题意知:AP=2t,CQ=t,则PC=10-2t
由AB⊥BC,PE⊥BC得PE∥AB
∴
| PE |
| AB |
| PC |
| AC |
即:
| PE |
| 6 |
| 10-2t |
| 10 |
∴PE=
| 3 |
| 5 |
| 6 |
| 5 |
又∵S△ABC=
| 1 |
| 2 |
∴S=S△ABC-S△PCQ=24-
| 1 |
| 2 |
| 6 |
| 5 |
| 3 |
| 5 |
即:S=
| 3 |
| 5 |
(2)假设四边形ABQP与△CPQ的面积相等,则有:
| 3 |
| 5 |
即:t2-5t+20=0
∵b2-4ac=(-5)2-4×1×20<0
∴方程无实根
∴在P、Q两点移动的过程中,四边形ABQP与△CPQ的面积不能相等.


练习册系列答案
相关题目

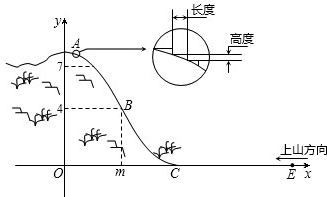 试求索道的最大悬空高度.
试求索道的最大悬空高度.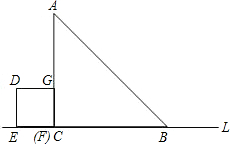 1cm的速度作匀速运动,最后点E与点B重合.
1cm的速度作匀速运动,最后点E与点B重合. 不存在,请说明理由.
不存在,请说明理由.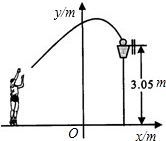 单位:m).请你根据所得的解析式,回答下列问题:
单位:m).请你根据所得的解析式,回答下列问题: