题目内容
【题目】三角形ABC(记作△ABC)在8×8方格中,位置如图所示,A(﹣2,1),B(﹣1,4).
(1)请你在方格中建立直角坐标系,并写出C点的坐标;
(2)把△ABC向上平移2个单位长度,再向右平移3个单位长度,请你画出平移后的△A1B1C1,若△ABC内部一点P的坐标为(a,b),则点P的对应点P1的坐标是 .
(3)在x轴上存在一点D,使△DBC的面积等于3,则点D的坐标为 .

【答案】(1)见详解,(2,1);(2)(a+3,b+2);(3)点D的坐标为(1,0)
【解析】
(1)根据点A、B的坐标和直角坐标系的特点建立直角坐标系;
(2)分别将点A、B、C向上平移2个单位长度,再向右平移3个单位长度,然后顺次连接各点,并写出点P的对应点P1的坐标;
(3)根据三角形的面积求出D到BC的距离,然后根据D到BC的距离求出点D的坐标即可.
解:(1)直角坐标系如图所示,
C点坐标(2,1);
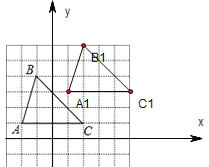
(2)△A1B1C1如图所示,
点P1坐标(a+3,b+2),
故答案为:(a+3,b+2);
(3)BC=![]() =
=![]() ,
,
设D到BC的距离为h,则
S△DBC=![]() ·BC·h=
·BC·h=![]() h=3,
h=3,
解得:h=![]() ,
,
即D到BC的距离为![]() ,
,
D在点(1,0)时,
CD=![]() =
=![]() ,且CD⊥BC,
,且CD⊥BC,
∴点D的坐标为(1,0).

练习册系列答案
相关题目