Question

【题目】在正方形中，动点分别从两点同时出发，以相同的速度在直线上移动；

(1)如图①,当分别移动到边的延长线上时，连接和与的关系为____ ；

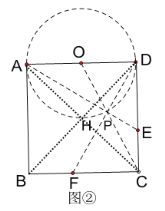
(2)如图②，己知正方形的边长为点和分别从点同时出发，以相同的速度沿方向向终点和运动，连接和，交于点，请你画出点运动路线的草图，试求出线段的最小值．

(3)如图③，在(2)的条件下，求周长的最大值；

Answer 1

【答案】（1）AE＝DF，AE⊥DF；（2）点运动路线见解析；线段CP的最小值为；（3）△APD周长的最大值为．

【解析】

（1）根据正方形的性质利用SAS证明△ADE≌△DCF，可得AE＝DF，∠DAE＝∠CDF，延长FD交AE于点G，求出∠ADG＋∠DAE＝90°即可；

（2）根据AE⊥DF可知点P在以AD为直径的圆弧上，当O、C、P三点共线时，线段CP最小，求出OC即可得到线段CP的最小值；

（3）如图③，以AD为斜边向外作等腰直角△ADG，过点G作GM⊥AE于M，GN⊥FD交FD的延长线于点N，连接GP，首先证明△AMG≌△DNG，四边形GMPN是正方形，然后求出PA＋PD＝2GM，且GM的最大值＝AG＝，再由三角形周长公式可得答案．

解：（1）∵四边形ABCD是正方形，

∴AD＝DC，∠ADE＝∠DCF＝90°，

∵动点E，F分别从D，C两点同时出发，以相同的速度在直线DC，CB上移动，

∴DE＝CF，

∴△ADE≌△DCF（SAS），

∴AE＝DF，∠DAE＝∠CDF，

延长FD交AE于点G，如图①所示，则∠CDF＋∠ADG＝90°，

∴∠ADG＋∠DAE＝90°，

∴∠AGD＝90°，

∴AE⊥DF，

故答案为：AE＝DF，AE⊥DF；

（2）由（1）可知AE⊥DF，

∴在点E、F的运动过程中，∠APD始终是90°，

∴点P在以AD为直径的圆弧上，即劣弧DH，如图所示，

设圆心为O，连接OC，则O、C、P三点共线时，线段CP最小，

∵圆心O为AD中点，正方形的边长为4，

∴OA＝OD＝OP＝2，

∴OC＝，

∴线段CP的最小值为：；

（3）如图③，以AD为斜边向外作等腰直角△ADG，过点G作GM⊥AE于M，GN⊥FD交FD的延长线于点N，连接GP，

∵∠GMP＝∠MPN＝∠N＝90°，

∴四边形GMPN是矩形，

∴∠MGN＝∠AGD＝90°，

∴∠AGM＝∠DGN，

∵∠AMG＝∠DNG＝90°，AG＝DG，

∴△AMG≌△DNG（AAS），

∴AM＝DN，MG＝NG，

∴矩形GMPN是正方形，

∴PA＋PD＝PM＋AM＋PN－DN＝PM＋PN＝2PM＝2GM，

∵GM≤AG，

∴GM的最大值＝AG＝，

∴PA＋PD的最大值为，

∴△APD周长的最大值为：．