题目内容
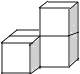
【题目】如图1所示,已知:点A(﹣2,﹣1)在双曲线C:y= ![]() 上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1 , l2于M,N两点.
上,直线l1:y=﹣x+2,直线l2与l1关于原点成中心对称,F1(2,2),F2(﹣2,﹣2)两点间的连线与曲线C在第一象限内的交点为B,P是曲线C上第一象限内异于B的一动点,过P作x轴平行线分别交l1 , l2于M,N两点.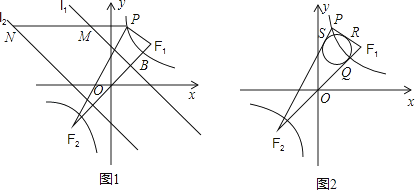
(1)求双曲线C及直线l2的解析式;
(2)求证:PF2﹣PF1=MN=4;
(3)如图2所示,△PF1F2的内切圆与F1F2 , PF1 , PF2三边分别相切于点Q,R,S,求证:点Q与点B重合.(参考公式:在平面坐标系中,若有点A(x1 , y1),B(x2 , y2),则A、B两点间的距离公式为AB= ![]() .)
.)
【答案】
(1)
解:把A(﹣2,﹣1)代入y= ![]() 中得:
中得:
a=(﹣2)×(﹣1)=2,
∴双曲线C:y= ![]() ,
,
∵直线l1与x轴、y轴的交点分别是(2,0)、(0,2),它们关于原点的对称点分别是(﹣2,0)、(0,﹣2),
∴l2:y=﹣x﹣2
(2)
解:设P(x, ![]() ),
),
由F1(2,2)得:PF12=(x﹣2)2+( ![]() ﹣2)2=x2﹣4x+
﹣2)2=x2﹣4x+ ![]() ﹣
﹣ ![]() +8,
+8,
∴PF12=(x+ ![]() ﹣2)2,
﹣2)2,
∵x+ ![]() ﹣2=
﹣2= ![]() =
= ![]() >0,
>0,
∴PF1=x+ ![]() ﹣2,
﹣2,
∵PM∥x轴
∴PM=PE+ME=PE+EF=x+ ![]() ﹣2,
﹣2,
∴PM=PF1,
同理,PF22=(x+2)2+( ![]() +2)2=(x+
+2)2=(x+ ![]() +2)2,
+2)2,
∴PF2=x+ ![]() +2,PN=x+
+2,PN=x+ ![]() +2
+2
因此PF2=PN,
∴PF2﹣PF1=PN﹣PM=MN=4
(3)
解:
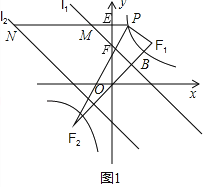
△PF1F2的内切圆与F1F2,PF1,PF2三边分别相切于点Q,R,S,
∴ 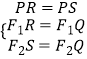 PF2﹣PF1=QF2﹣QF1=4
PF2﹣PF1=QF2﹣QF1=4
又∵QF2+QF1=F1F2=4 ![]() ,QF1=2
,QF1=2 ![]() ﹣2,
﹣2,
∴QO=2,
∵B( ![]() ,
, ![]() ),
),
∴OB=2=OQ,
所以,点Q与点B重合
【解析】(1)利用点A的坐标求出a的值,根据原点对称的性质找出直线l2上两点的坐标,求出解析式;(2)设P(x, ![]() ),利用两点距离公式分别求出PF1、PF2、PM、PN的长,相减得出结论;(3)利用切线长定理得出
),利用两点距离公式分别求出PF1、PF2、PM、PN的长,相减得出结论;(3)利用切线长定理得出 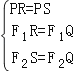 ,并由(2)的结论PF2﹣PF1=4得出PF2﹣PF1=QF2﹣QF1=4,再由两点间距离公式求出F1F2的长,计算出OQ和OB的长,得出点Q与点B重合.此题主要考查了圆的综合应用以及反比例函数的性质等知识,将代数与几何融合在一起,注意函数中线段的长可以利用本题给出的两点距离公式解出,也可以利用勾股定理解出;解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.
,并由(2)的结论PF2﹣PF1=4得出PF2﹣PF1=QF2﹣QF1=4,再由两点间距离公式求出F1F2的长,计算出OQ和OB的长,得出点Q与点B重合.此题主要考查了圆的综合应用以及反比例函数的性质等知识,将代数与几何融合在一起,注意函数中线段的长可以利用本题给出的两点距离公式解出,也可以利用勾股定理解出;解答本题需要我们熟练各部分的内容,对学生的综合能力要求较高,一定要注意将所学知识贯穿起来.
【考点精析】本题主要考查了反比例函数的性质的相关知识点,需要掌握性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大才能正确解答此题.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案