题目内容
【题目】求证：全等三角形对应边上的中线相等（请根据图形，写出已知、求证、证明）
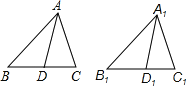
已知：
求证：
证明：
【答案】详见解析.
【解析】
首先根据△ABC≌△A1B1C1，可得AB=A1B1，BC=B1C1，∠B=∠B1，进而得到中线BD=B1D1，再证明△ABD≌△A1B1D1可得AD=A1D1
．
已知：△ABC≌△A1B1C1 ，AD、A1D1分别是对应边BC、B1C1的中线
求证：AD=A1D1
证明：∵△ABC≌△A1B1C1
∴AB=A1B1
BC=B1C1
∠B=∠B1
∵AD、A1D1分别是对应边BC、B1C1的中线
∴BD=
BC；
B1D1=B1C1
∴BD=B1D1
在△ABD和△A1B1D1中:
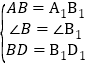
∴△ABD≌△A1B1D1（SAS）
∴AD=A1D1
练习册系列答案
相关题目
