Question

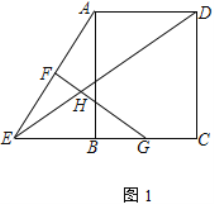
【题目】如图1，在矩形ABCD中，E是CB延长线上一个动点，F、G分别为AE、BC的中点，FG与ED相交于点H

(1) 求证：HE＝HG

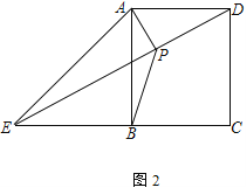
(2) 如图2，当BE＝AB时，过点A作AP⊥DE于点P连接BP，求的值

(3) 在(2)的条件下，若AD＝2，∠ADE＝30°，则BP的长为______________

Answer 1

【答案】（1）证明见解析；（2）；（3）BP的长为

【解析】试题分析：（1）延长BC至M，且使CM＝BE，通过三角形全等对应角相等，得出 G为EM的中点，由中位线性质得出∠HGE＝∠AMB＝∠HEG，由等角对等边得出HE＝HG；（2）通过做辅助线得出三角形全等，对应边相等，即可求比值；（3）由∠ADE＝∠CED＝30°

∴CE＝CD得出CE＝CD，由BE＋BC＝CD＋2＝CD，得CD＝，由DE＝，∠ADE＝30°，得AP＝1，DP＝，

试题解析：（1）延长BC至M，且使CM＝BE，连接AM，

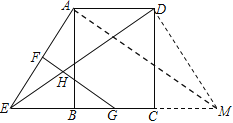
∴△ABM≌△DCE（SAS）

∴∠DEC＝∠AMB

∵EB＝CM，BG＝CG

∴G为EM的中点

∴FG为△AEM的中位线

∴FG∥AM

∴∠HGE＝∠AMB＝∠HEG

∴HE＝HG

(2) 过点B作BQ⊥BP交DE于Q

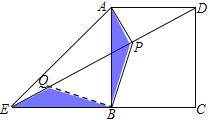
由八字型可得：∠BEQ＝∠BAP

∴△BEQ≌△BAP（ASA）

∴PA＝QE

∴

(3) ∵∠ADE＝∠CED＝30°

∴CE＝CD

∴BE＋BC＝CD＋2＝CD，CD＝

∴DE＝2CD＝

∵∠ADE＝30°

∴AP＝EQ＝1，DP＝

∴PQ＝－1－＝

∴BP＝