题目内容
【题目】为了落实党的“精准扶贫”政策,A.,B两城决定向C,D两乡运送肥料以支持农村生产,已知A,B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C,D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C, D两乡运肥料的费用分别为15元/吨和24元/吨。现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
【答案】(1)A城和B城分别有200吨和300吨肥料;(2)10040元;(3)当0<a4时,A城化肥全部运往D乡,B城运往C城240吨,运往D乡60吨,运费最少; 当4<a<6时,A城化肥全部运往C乡,B城运往C城40吨,运往D乡260吨,运费最少.
【解析】
(1)根据A,B两城共有肥料500吨,其中A城肥料比B城少100吨,列方程或方程组得答案;
(2)设从A城运往C乡肥料x吨,用含x的代数式分别表示出从A运往运往D乡的肥料吨数,从B城运往C乡肥料吨数,及从B城运往D乡肥料吨数,根据:运费=运输吨数×运输费用,得一次函数解析式,利用一次函数的性质得结论;
(3)列出当A城运往C乡的运费每吨减少a(0<a<6)元时的一次函数解析式,利用一次函数的性质讨论,得结论.
(1)设A城有化肥a吨,B城有化肥b吨
根据题意,得![]()
解得![]()
答:A城和B城分别有200吨和300吨肥料;
(2)设从A城运往C乡肥料x吨,则运往D乡(200x)吨
从B城运往C乡肥料(240x)吨,则运往D乡(60+x)吨
如总运费为y元,根据题意,
则:y=20x+25(200x)+15(240x)+24(60+x)
=4x+10040
由于函数是一次函数,k=4>0
所以当x=0时,运费最少,最少运费是10040元.
(3)从A城运往C乡肥料x吨,由于A城运往C乡的运费每吨减少a(0<a<6)元,
所以y=(20a)x+25(200x)+15(240x)+24(60+x)
=(4a)x+10040
当0<a4时,∵4a0
∴当x=0时,运费最少;
当4<a<6时,∵4a<0
∴当x=240时,运费最少.
所以:当0<a4时,A城化肥全部运往D乡,B城运往C城240吨,运往D乡60吨,运费最少;
当4<a<6时,A城化肥全部运往C乡,B城运往C城40吨,运往D乡260吨,运费最少.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案【题目】如图,用正方形是墩垒石梯,下图分别表示垒到一、二阶梯时的情况,那么照这样垒下去
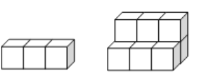
一级 二级
①填出下表中未填的两空,观察规律。
阶梯级数 | 一级 | 二级 | 三级 | 四级 |
石墩块数 | 3 | 9 |
②到第n级阶梯时,共用正方体石墩_______________块(用n的代数式表示)
【题目】为了了解某校学生的课外阅读情况,随机抽查了![]() 名学生周阅读用时数,结果如下表:
名学生周阅读用时数,结果如下表:
周阅读用时数(小时) | 4 | 5 | 8 | 12 |
学生人数(人) | 3 | 4 | 2 | 1 |
则关于这![]() 名学生周阅读所用时间,下列说法正确的是( )
名学生周阅读所用时间,下列说法正确的是( )
A. 中位数是![]() B. 众数是
B. 众数是![]() C. 平均数是
C. 平均数是![]() D. 方差是
D. 方差是![]()