��Ŀ����
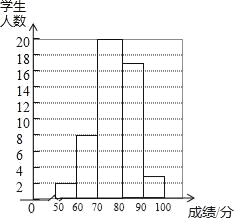
����Ŀ������ʦ���������У��ȫ֪ʶ�������ɼ����ɼ���s��ʾ������Ϊ100�֣���Ϊ5�飬��1�飺50��x��60����2�飺60��x��70��������5�飺90��x��100������������ͼ��ʾ��Ƶ�ʷֲ�����Ƶ���ֲ�ֱ��ͼ������������
��1���벹ȫƵ�ʷֲ�����Ƶ���ֲ�ֱ��ͼ��
��2������ʦ�ӵ�1��͵�5���ѧ���У������ȡ����ѧ������̸�������1��������һ��ѧ�����鵽�ĸ��ʣ�
��3����ӵ�1��͵�5��������鵽������ѧ���ijɼ��ֱ�Ϊm��n�����¼���|m��n|��10���ĸ��ʣ�
������ | �ɼ� | Ƶ�� | Ƶ�� |
��1�� | 50��s��60 | 0.04 | |
��2�� | 60��s��70 | 8 | 0.16 |
��3�� | 70��s��80 | 0.4 | |
��4�� | 80��s��90 | 17 | 0.34 |
��5�� | 90��s��100 | 3 | 0.06 |
�ϼ� | 1 |

���𰸡���1����ȫƵ���ֲ�ֱ��ͼ����������2��Ƶ�ʷֲ������貹�����ϵ���2��20��50������2����1��������һ��ѧ�����鵽�ĸ���Ϊ![]() ����3���¼���|m��n|��10���ĸ���Ϊ
����3���¼���|m��n|��10���ĸ���Ϊ![]() ��
��
��������
��1�����ݵ�2���Ƶ����Ƶ����ʽ���ѧ����������Ȼ�������Ӧ��Ƶ���뼴�ɣ��ٸ���Ƶ��֮�͵���1���Ȼ��ȫͳ��ͼ��
��2��������״ͼ��Ȼ����ݸ��ʹ�ʽ��ʽ���㼴�ɵý⣻
��3��������ֻ࣬�б��鵽�����˶���ͬһ�鷽������|m-n|��10��Ȼ����ݸ��ʹ�ʽ��ʽ���㼴�ɵý⣮
�⣺��1��ѧ��������Ϊ��8��0.16=50��
��1��Ƶ����50��0.04=2��
��3��Ƶ����50��0.4=20��
Ƶ��֮��Ϊ50��Ƶ��֮��Ϊ1��
��ȫƵ���ֲ�ֱ��ͼ��ͼ��ʾ��
Ƶ�ʷֲ������貹�����ϵ���2��20��50����
��2���������⻭����״ͼ���£�
��1�鹲2�ˣ�����ֱ��Ϊa1��a2����5�鹲3�ˣ�����ֱ��Ϊb1��b2��b3��

һ����20���������1��������һ��ѧ�����鵽�������14�֣�
�ʵ�1��������һ��ѧ�����鵽�ĸ���ΪP=![]() =
=![]() ��
��
��3�������鵽��2��ѧ�������Ե�1�飬����ͷ�Ϊ50����߷ֲ���60������|m��n|��10���������⣻
���鵽��2��ѧ�������Ե�5�飬����ͷ�Ϊ90����߷ֲ�����100������|m��n|��10���������⣻
���鵽��2��ѧ��һ�����Ե�1�飬��һ�����Ե�5�飬����30��|m��n|��50�����������⣬
�ɴˣ����鵽��2��ѧ��������ͬһ�飬
�ʣ��¼���|m��n|��10���ĸ���ΪP=![]() =
=![]() ��
��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�