题目内容
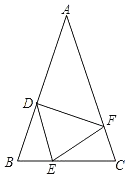
【题目】已知：如图，△ABC中，AD是高，AE平分∠BAC，∠B＝50°，∠C＝80°.求∠DAE的度数.
【答案】∠DAE=15°.
【解析】
根据三角形的内角和定理，可求得∠BAC的度数，由AE是∠BAC的平分线，可得∠EAC的度数，在直角△ADC中，可求出∠DAC的度数，所以根据∠DAE＝∠EAC﹣∠DAC即可得出.
解：∵△ABC中，∠B＝50°，∠C＝80°，
∴∠BAC＝180°﹣∠B﹣∠C＝180°﹣50°﹣80°＝50°，
∵AE是∠BAC的平分线，
∴∠EAC＝
∠BAC＝25°，
∵AD是BC边上的高，
∴在直角△ADC中，∠DAC＝90°﹣∠C＝90°﹣80°＝10°，
∴∠DAE＝∠EAC﹣∠DAC＝25°﹣10°＝15°.
练习册系列答案
黄冈冠军课课练系列答案
相关题目
【题目】王老师将本班的“校园安全知识竞赛”成绩（成绩用s表示，满分为100分）分为5组，第1组：50≤x＜60，第2组：60≤x＜70，…，第5组：90≤x＜100．并绘制了如图所示的频率分布表和频数分布直方图（不完整）．
（1）请补全频率分布表和频数分布直方图；
（2）王老师从第1组和第5组的学生中，随机抽取两名学生进行谈话，求第1组至少有一名学生被抽到的概率；
（3）设从第1组和第5组中随机抽到的两名学生的成绩分别为m、n，求事件“|m﹣n|≤10”的概率．
分组编号 | 成绩 | 频数 | 频率 |
第1组 | 50≤s＜60 | 0.04 | |
第2组 | 60≤s＜70 | 8 | 0.16 |
第3组 | 70≤s＜80 | 0.4 | |
第4组 | 80≤s＜90 | 17 | 0.34 |
第5组 | 90≤s≤100 | 3 | 0.06 |
合计 | 1 |
