Question

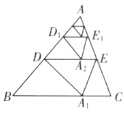
【题目】如图，将沿着过中点D的直线折叠，使点A落在边上的处，称为第1次操作，折痕到的距离记为，还原纸片后，再将沿着过中点的直线折叠，使点A落在边上的处，称为笫2次操作，折痕到的距离记为.按上述方法不断操作下去……经过第2015次操作后得到的折痕到的距离记为，若，则的值为（ ）

A. B. C. D.

Answer 1

【答案】B

【解析】

根据中点的性质及折叠的性质可得DA=DA'=DB，从而可得∠ADA'=2∠B，结合折叠的性质，∠ADA'=2∠ADE，可得∠ADE=∠B，继而判断DE∥BC，得出DE是△ABC的中位线，证得A A⊥BC，得到A A=2，求出=2-1=1，同理h=2-，推理得到答案．

连接AA，

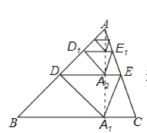
由折叠的性质可得：A A⊥DE,DA=D A，

又∵D是AB中点，

∴DA=DB，

∴DB=D A，

∴∠B AD=∠B，

∴∠AD A=2∠B，

又∵∠AD A=2∠ADE，

∴∠ADE=∠B，

∴DE∥BC，

∴A A⊥BC，

∴A A=2，

∴=21=1，

同理,h=2,h=2，

∴经过第n次操作后得到的折痕DE到BC的距离，

∴，

故选B.