题目内容
【题目】如图,抛物线y=ax2+bx﹣2与y轴的交点为A,抛物线的顶点为B(1,﹣3).
(1)求出抛物线的解析式;
(2)点P为x轴上一点,当三角形PAB的周长最小时,求出点P的坐标;
(3)水平移动抛物线,新抛物线的顶点为C,两抛物线的交点为D,当O,C,D在一条直线上时,请直接写出平移的距离.

【答案】(1) y=(x﹣1)2﹣3=x2﹣2x﹣2 (2) P(![]() ,0) (3) 平移距离为2或3
,0) (3) 平移距离为2或3
【解析】
(1)根据题意可得点A的坐标为(0,﹣2),根据顶点坐标为(1,﹣3),可得设抛物线解析式y=a(x﹣1)2﹣3把A点的坐标代入求得a值,即可得抛物线的解析式;(2)当PA+PB最小时,△ABP的周长最小,作A点关于x轴的对称点A'(0,2),连接A'B,用待定系数法求得直线A'B的解析式,直线A'B与x轴的交点坐标即为点P的坐标;(3)设抛物线向右平移m个单位,得到新的抛物线的顶点C(1+m,-3),由此可得新抛物线的解析式,把两个抛物线的解析式联立组成方程组,解方程组求得点D的坐标,再求得直线OC的解析式,因O、C、D三点共线,可得以m为未知数的方程,解方程求得m的值即可.
(1)根据题意得:A(0,﹣2),
设抛物线解析式y=a(x﹣1)2﹣3过点A(0,﹣2),
∴﹣2=a﹣3,
∴a=1,
∴抛物线解析式y=(x﹣1)2﹣3=x2﹣2x﹣2;
(2)∵A(0,﹣2),B(1,﹣3),
∴AB=![]() ,
,
∵△ABP的周长=PA+PB+AB=PA+PB+![]() ,
,
∴当PA+PB最小时,△ABP的周长最小;
作A点关于x轴的对称点A'(0,2),连接A'B,
设直线A'B解析式y=kx+b,
根据题意得:![]() ,
,
解得:k=﹣5,b=2
∴直线A'B的解析式y=﹣5x+2;
当y=0时,x=![]() ,
,
∴P(![]() ,0);
,0);
(3)设向右平移m个单位长度,则所得新的抛物线的顶点C(1+m,-3),
∴平移后抛物线解析式y=(x﹣1﹣m)2﹣3,
∴C(1+m,﹣3),
∴根据题意可得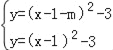 ,
,
∴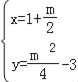 ,
,
∴D(1+![]() ,
,![]() );
);
∵C(1+m,﹣3,),O(0,0),
∴直线CO解析式y=![]() x,
x,
∵O,C,D三点共线,
∴![]() =
=![]() ,
,
解得:m1=0(不合题意舍去),m2=﹣3,m3=2;
∴向右平移2个单位长度,或向左平移3个单位长度,O,C,D三点共线.
∴平移距离为2或3.







