题目内容
 如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c和直线y=x+2都经过A、B两点,且点A在y轴上,点B的纵坐标为5,抛物线的顶点为C.
如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c和直线y=x+2都经过A、B两点,且点A在y轴上,点B的纵坐标为5,抛物线的顶点为C.(1)求抛物线的表达式,并写出顶点C的坐标;
(2)若E、F是x轴正半轴上的两个动点(点E在点F的左侧),且EF=2,求四边形AEFB周长的最小值及此时点E的坐标;
(3)设抛物线的对称轴与直线AB相交于点M,点B关于直线MC的对称点为B',点P是以M为圆心,MC为半径的圆上的一个动点,请你直接写出BP+
| 2 |
考点:二次函数综合题
专题:压轴题
分析:(1)根据题意求得点A的坐标为(0,2),点B的坐标为(3,5).把点A、B的坐标分别代入函数解析式,利用方程组来求b、c的值;根据所求得的函数解析式来求顶点C的坐标;
(2)AB、EF的长为定值,当四边形AEFB的周长最小时,AE+BF的值最小.
如图,作点A关于x轴的对称点A',连结A'E,作BH⊥y轴,垂足为点H,在BH上截取BD=2,连结DE.构建?BDEF,则BF=DE.当点E在直线A'D上时,A'E+DE=A′D=
=
=5
.则四边形AEFB周长的最小值=A′D+AB+EF=2+8
.此时
=
,所以OE=
=
.
(3)根据A、B的坐标求出AM、BM的长,再求出点M的坐标,从而得到⊙M的半径为2,取MB的中点N,连接QB、QN、QB′,然后利用两边对应成比例夹角相等两三角形相似求出△MNP和△MPB相似,再根据相似三角形对应边成比例求出2PN=
′P,然后根据三角形任意两边之和大于第三边判断出Q、N、B′三点共线时BP+
B′P最小,然后利用勾股定理列式计算即可得解.
(2)AB、EF的长为定值,当四边形AEFB的周长最小时,AE+BF的值最小.
如图,作点A关于x轴的对称点A',连结A'E,作BH⊥y轴,垂足为点H,在BH上截取BD=2,连结DE.构建?BDEF,则BF=DE.当点E在直线A'D上时,A'E+DE=A′D=
| A′H2+HD2 |
| 72+12 |
| 2 |
| 2 |
| OE |
| HD |
| A′O |
| A′H |
| HD•A′O |
| A′H |
| 2 |
| 7 |
(3)根据A、B的坐标求出AM、BM的长,再求出点M的坐标,从而得到⊙M的半径为2,取MB的中点N,连接QB、QN、QB′,然后利用两边对应成比例夹角相等两三角形相似求出△MNP和△MPB相似,再根据相似三角形对应边成比例求出2PN=
| 2 |
| 2 |
解答: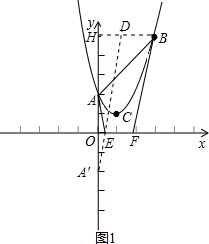 解:(1)将x=0代入y=x+2,得y=2,
解:(1)将x=0代入y=x+2,得y=2,
∴点A的坐标为(0,2).
将y=5代入y=x+2,得x=3,
∴点B的坐标为(3,5).
∵抛物线y=x2+bx+c经过A、B两点,
∴
,
解得
.
∴抛物线的表达式为y=x2-2x+2.
∵y=x2-2x+2=(x-1)2+1,
∴顶点C的坐标为(1,1).
(2)∵AB、EF的长为定值,
∴当四边形AEFB的周长最小时,AE+BF的值最小.
如图,作点A关于x轴的对称点A',连结A'E,则AE=A'E.
作BH⊥y轴,垂足为点H,在BH上截取BD=2,连结DE.
易证四边形BDEF是平行四边形,则BF=DE.
∴AE+BF=A'E+DE.
当点E在直线A'D上时,A'E+DE的值最小.
∴AE+BF的最小值为A'D,A′D=
=
=5
.
又∵AB=
=
=3
,EF=2,
∴四边形AEFB周长的最小值=A′D+AB+EF=2+8
.
此时∵OE∥HD,
∴
=
,
∴OE=
=
.
∴点E的坐标为(
,0);
(3)BP+
B′P的最小值为2+2
.
理由如下:如图2,∵A(0,2),B(3,5),
∴直线AB的解析式为:y=x+2.
∵顶点C的坐标为(1,1),
∴M(1,3)
∴AM=
,MC=2,
∴圆M的半径为2.
取MB的中点N,连接PB、PN、PB′,
则MN=
MB=
,B′M=BM,
∵
=
=
,∠PMN=∠B′MP,
∴△MNP∽△MPB′,
∴
=
=
,
∴
B′P=2PN.
由三角形三边关系,当P、N、B′三点共线时BP+
B′P最小,
此时点P是直线BB′与圆M的切点.则
BP+
B′P最小值=BP+2PN=BP+BM=2+2
.
 解:(1)将x=0代入y=x+2,得y=2,
解:(1)将x=0代入y=x+2,得y=2,∴点A的坐标为(0,2).
将y=5代入y=x+2,得x=3,
∴点B的坐标为(3,5).
∵抛物线y=x2+bx+c经过A、B两点,
∴
|
解得
|
∴抛物线的表达式为y=x2-2x+2.
∵y=x2-2x+2=(x-1)2+1,
∴顶点C的坐标为(1,1).
(2)∵AB、EF的长为定值,
∴当四边形AEFB的周长最小时,AE+BF的值最小.
如图,作点A关于x轴的对称点A',连结A'E,则AE=A'E.
作BH⊥y轴,垂足为点H,在BH上截取BD=2,连结DE.
易证四边形BDEF是平行四边形,则BF=DE.
∴AE+BF=A'E+DE.
当点E在直线A'D上时,A'E+DE的值最小.
∴AE+BF的最小值为A'D,A′D=
| A′H2+HD2 |
| 72+12 |
| 2 |
又∵AB=
| AH2+BH2 |
| 32+32 |
| 2 |
∴四边形AEFB周长的最小值=A′D+AB+EF=2+8
| 2 |
此时∵OE∥HD,
∴
| OE |
| HD |
| A′O |
| A′H |
∴OE=
| HD•A′O |
| A′H |
| 2 |
| 7 |
∴点E的坐标为(
| 2 |
| 7 |
(3)BP+
| 2 |
| 2 |
理由如下:如图2,∵A(0,2),B(3,5),
∴直线AB的解析式为:y=x+2.
∵顶点C的坐标为(1,1),
∴M(1,3)

∴AM=
| 2 |
∴圆M的半径为2.
取MB的中点N,连接PB、PN、PB′,
则MN=
| 1 |
| 2 |
| 2 |
∵
| MN |
| PM |
| PM |
| B′M |
| ||
| 2 |
∴△MNP∽△MPB′,
∴
| PN |
| B′P |
| MN |
| MP |
| ||
| 2 |
∴
| 2 |
由三角形三边关系,当P、N、B′三点共线时BP+
| 2 |
此时点P是直线BB′与圆M的切点.则
BP+
| 2 |
| 2 |
点评:本题是二次函数综合题型,主要利用了二次函数解析式的转化,联立两函数解析式求交点坐标,勾股定理的应用,三角形的面积的求解,相似三角形的判定与性质,本题难点在于(3),作辅助线构造出相似三角形并得到与
B′P相等的线段是解题的难点,也是关键.
| 2 |

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
用配方法解方程x2+10x+9=0,配方正确的是( )
| A、(x+5)2=16 |
| B、(x+5)2=34 |
| C、(x-5)2=16 |
| D、(x+5)2=25 |
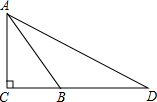 如图,在Rt△ABC中,∠C=90°,AC=8,AC:AB=4:5,延长CB到D使得BD=AB,连接AD,求AD的长.
如图,在Rt△ABC中,∠C=90°,AC=8,AC:AB=4:5,延长CB到D使得BD=AB,连接AD,求AD的长.