题目内容
【题目】如图,AD为△ABC的中线,BE为△ABD的中线. 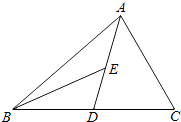
(1)∠ABE=15°,∠BAD=40°,求∠BED的度数;
(2)在△BED中作BD边上的高;
(3)若△ABC的面积为40,BD=5,则△BDE中BD边上的高为多少?
【答案】
(1)解:∵∠BED是△ABE的外角,
∴∠BED=∠ABE+∠BAD=15°+40°=55°
(2)解:过E作BC边的垂线,F为垂足,则EF为所求
(3)解:过A作BC边的垂线AG,
∴AD为△ABC的中线,BD=5,
∴BC=2BD=2×5=10,
∵△ABC的面积为40,
∴ ![]() BCAG=40,即
BCAG=40,即 ![]() ×10AG=40,解得AG=8,
×10AG=40,解得AG=8,
∵EF⊥BC于F,
∴EF∥AG,
∵E为AD的中点,
∴EF是△AGD的中位线,
∴EF= ![]() AG=
AG= ![]() ×8=4.
×8=4.
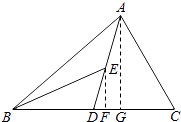
【解析】(1)根据三角形内角与外角的性质解答即可;(2)过E作BC边的垂线即可;(3)过A作BC边的垂线AG,再根据三角形中位线定理求解即可.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对三角形的外角的理解,了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.

练习册系列答案
相关题目
【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
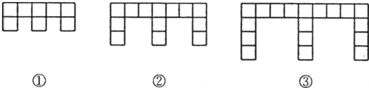
(1)观察图形,填写下表:
图形 | ① | ② | ③ |
正方形的个数 | 8 |
|
|
图形的周长 | 18 |
|
|
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .