题目内容
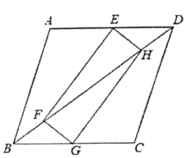
【题目】已知正方形![]() ,
,![]() 经过点
经过点![]() ,
,![]() ,且与
,且与![]() 边相切于点
边相切于点![]() ,连接
,连接![]() .
.
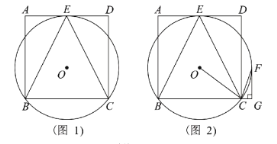
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,点
,点![]() 是圆
是圆![]() 上一点
上一点![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
①求证:![]() 是
是![]() 的切线;
的切线;
②若正方形![]() 的边长为
的边长为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)先说四边形![]() 为矩形,然后再说明
为矩形,然后再说明![]() ,BE=CH,即可完成证明;
,BE=CH,即可完成证明;
(2)①先根据等腰三角形的性质得到![]() ,再说明
,再说明![]() ;最后由
;最后由![]() 即可完成证明;
即可完成证明;
②先求出HC的长,设![]() 的半径为
的半径为![]() ,再利用垂径定理和勾股定理求得R=5,然后再说明四边形
,再利用垂径定理和勾股定理求得R=5,然后再说明四边形![]() 是矩形,进一步求得FG和CG的长,最后根据正切定义解答即可.
是矩形,进一步求得FG和CG的长,最后根据正切定义解答即可.
(1)证明:如图,连接![]() 并延长交
并延长交![]() 于
于![]()
![]() 与
与![]() 相切,
相切,![]() ,
,
![]()
![]() 四边形
四边形![]() 为正方形,
为正方形,
![]()
![]() 四边形
四边形![]() 为矩形,
为矩形,
![]() ,
,![]()
同理,![]()
![]() ,
,
![]() ,
,
![]()
(2)①证明:如图,连接![]()
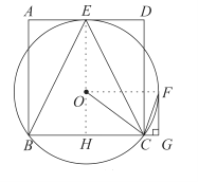
![]() ,
,
![]()
又![]() 平分,
平分,
![]()
![]() ,
,
![]()
![]()
又![]() ,
,
![]()
![]()
![]()
故![]() 是
是![]() 的切线
的切线
②解:![]() 四边形
四边形![]() 为矩形,
为矩形,
![]()
由![]() 知
知![]()
设![]() 的半径为
的半径为![]() ,则
,则![]() ,
,![]()
在![]() 中,
中,![]()
![]()
解之得:![]()
![]()
![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,![]()
![]()
在![]() 中,
中,![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目