题目内容
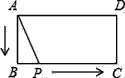
【题目】如图1,已知二次函数y=x2+bx+c的图象与x 轴交于A(﹣1,0)、B(3,0)两点,与y 轴交于点C,顶点为D,对称轴为直线l.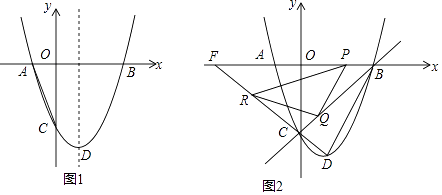
(1)求该二次函数的表达式;
(2)若点E 是对称轴l 右侧抛物线上一点,且S△ADE=2S△AOC , 求点E 的坐标;
(3)如图2,连接DC 并延长交x 轴于点F,设P 为线段BF 上一动点(不与B、F 重合),过点P 作PQ∥BD 交直线BC 于点Q,将直线PQ 绕点P 沿顺时针方向旋转45°后,所得的直线交DF 于点R,连接QR.请直接写出当△PQR 与△PFR 相似时点P 的坐标.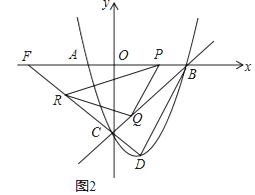
【答案】
(1)
解:将点A和点B的坐标代入抛物线的解析式得 ![]() ,解得
,解得 ![]() ,
,
∴二次函数的表达式为y=x2﹣2x﹣3;
(2)
解:设E(m,m2﹣2m﹣3),过点E作EM∥x轴,交AD于点M,(如图1)
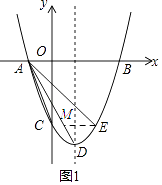
由y=x2﹣2x﹣3=( x﹣1)2﹣4得顶点D(1,﹣4),C(0,﹣3),
∴ ![]() ,
,
∴S△ADE=2S△AOC=3,
∵A(﹣1,0)、D(1,﹣4),
∴直线AD为:y=﹣2x﹣2,
∵E(m,m2﹣2m﹣3),
∴M( ![]() ,m2﹣2m﹣3),
,m2﹣2m﹣3),
∴EM= ![]() ,
,
∴S△ADE ![]() ×4×EM=2EM=m2﹣1=3,
×4×EM=2EM=m2﹣1=3,
解得m=±2(其中m=﹣2舍去),
∴E(2﹣3);
(3)
解:∵C(0,﹣3),D(1,﹣4),
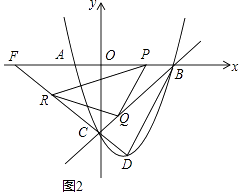
∴直线CD的解析式为:y=﹣x﹣3.
当y=0时,x=﹣3,
故F(0,﹣3),
∴OF=OC=3,
∴∠OFC=45°,即∠PFR=45°.
∵PQ∥BD,
∴∠FPQ≠90°,
∴∠FPR≠45°,
∴当△PQR 与△PFR 相似时:
△PQR∽△FRP,则
点P的坐标是:P1( ![]() ,0)、P2(0,0).
,0)、P2(0,0).
【解析】(1)由A、B两点的坐标,利用待定系数法可求得二次函数的表达式;(2)设E(m,m2﹣2m﹣3),过点E作EM∥x轴,交AD于点M,由条件可得△AOC的面积,从而可求得△ADE的面积,利用待定系数法可求得直线AD的解析式,则可用m表示出EM的长,从而可用m表示出△ADE的面积,从而可得到关于m的方程,可求得m的值;(3)由C、D坐标可求得直线CD的解析式,从而可求得F点坐标,可求得OF=OC,可得∠RFP=∠RPQ=45°,由△PQR 与△PFR 相似得到:△PQR∽△FRP 或△PQR∽△FPR,结合相似三角形的对应边成比例得到点P的坐标.
【考点精析】通过灵活运用确定一次函数的表达式和三角形的面积,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;三角形的面积=1/2×底×高即可以解答此题.