题目内容
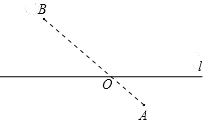
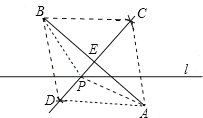
【题目】如图,已知直线l及其两侧两点A、B.

(1)在直线l上求一点O,使到A、B两点距离之和最短;
(2)在直线l上求一点P,使PA=PB;
(3)在直线l上求一点Q,使l平分∠AQB.
【答案】见解析
【解析】
试题分析:(1)根据两点之间线段最短,连接AB,线段AB交直线l于点O,则O为所求点;
(2)根据线段垂直平分线的性质连接AB,在作出线段AB的垂直平分线即可;
(3)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,由三角形全等的判定定理求出△BDQ≌△B′DQ,再由全等三角形的性质可得出∠BQD=∠B′QD,即直线l平分∠AQB.
解:(1)连接AB,线段AB交直线l于点O,
∵点A、O、B在一条直线上,
∴O点即为所求点;
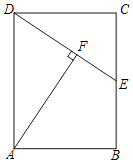
(2)连接AB,
分别以A、B两点为圆心,以任意长为半径作圆,两圆相交于C、D两点,连接CD与直线l相交于P点,
连接BD、AD、BP、AP、BC、AC,
∵BD=AD=BC=AC,
∴△BCD≌△ACD,
∴∠BED=∠AED=90°,
∴CD是线段AB的垂直平分线,
∵P是CD上的点,
∴PA=PB;
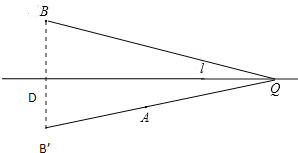
(3)作B关于直线l的对称点B′,连接AB′交直线l与点Q,连接BQ,
∵B与B′两点关于直线l对称,
∴BD=B′D,DQ=DQ,∠BDQ=∠B′DQ,
∴△BDQ≌△B′DQ,
∴∠BQD=∠B′QD,即直线l平分∠AQB.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .