题目内容
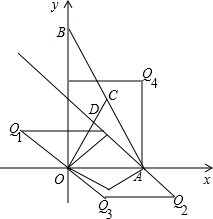
如图,在平面直角坐标系中,点A、B分别在x轴、y轴上,线段OA、OB的长(0A<OB)是方程组
的解,点C是直线y=2x与直线AB的交点,点D在线段OC上,OD=2
.
(1)求直线AB的解析式及点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

|
| 5 |
(1)求直线AB的解析式及点C的坐标;
(2)求直线AD的解析式;
(3)P是直线AD上的点,在平面内是否存在点Q,使以0、A、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.

(1)解方程组方程组
,
解得:
∵线段OA、OB的长(0A<OB)是方程组
的解,
∴OA=6,OB=12,
∴A(6,O),B(0,12),
设直线AB的解析为y=kx+b,
∴
∴直线AB:y=-2x+12,
联立
,
解得:
,
点C的坐标为(3,6);
(2)设点D:(a,2a),
由OD=2
:a2+(2a)2=(2
)2,
得:a=±2,
∵由图得,a>0,
∴a=2.
∴D(2,4),
设直线AD的解析式为y=kx+b
把A(6,0),D(2,4)代入得
,
解得
,
∴直线AD的解析式为y=-x+6;
(3)存在.
Q1(-3
,3
)
Q2(3
,-3
)
Q3(3,-3)
Q4(6,6)
|
解得:
|
∵线段OA、OB的长(0A<OB)是方程组
|
∴OA=6,OB=12,
∴A(6,O),B(0,12),
设直线AB的解析为y=kx+b,
∴
|
∴直线AB:y=-2x+12,
联立
|
解得:
|
点C的坐标为(3,6);
(2)设点D:(a,2a),
由OD=2
| 5 |
| 5 |
得:a=±2,
∵由图得,a>0,
∴a=2.
∴D(2,4),
设直线AD的解析式为y=kx+b
把A(6,0),D(2,4)代入得
|

解得
|
∴直线AD的解析式为y=-x+6;
(3)存在.
Q1(-3
| 2 |
| 2 |
Q2(3
| 2 |
| 2 |
Q3(3,-3)
Q4(6,6)


练习册系列答案
相关题目

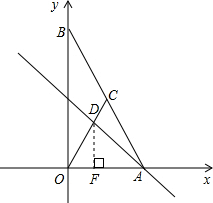
 点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0).
点B按顺时针方向旋转90°,得到线段BC.过点B作x轴的垂线交直线AC于点D.设点B坐标是(t,0).