题目内容
【题目】已知:如图,一次函数y=﹣2x与二次函数y=ax2+2ax+c的图象交于A、B两点(点A在点B的右侧),与其对称轴交于点C.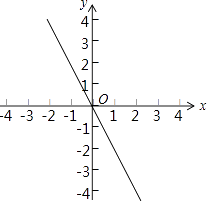
(1)求点C的坐标;
(2)设二次函数图象的顶点为D,点C与点D关于x轴对称,且△ACD的面积等于2.
①求二次函数的解析式;
②在该二次函数图象的对称轴上求一点P(写出其坐标),使△PBC与△ACD相似.
【答案】
(1)
解:∵y=ax2+2ax+c=a(x+1)2+c﹣a,
∴它的对称轴为x=﹣1.
又∵一次函数y=﹣2x与对称轴交于点C,
∴y=2.
∴C点的坐标为(﹣1,2)
(2)
解:①∵点C与点D 关于x轴对称,
∴点D的坐标为(﹣1,﹣2).
∴CD=4,
∵△ACD的面积等于2.
∴点A到CD的距离为1,C点与原点重合,点A的坐标为(0,0).
设二次函数为y=a(x+1)2﹣2过点A,则a=2,
∴y=2x2+4x.
②设P(﹣1,t).
交点B的坐标为(﹣3,6),D(﹣1,﹣2),C(﹣1,2),A(0,0),
则BC=2 ![]() ,PC=t﹣2,CD=4,AD=
,PC=t﹣2,CD=4,AD= ![]() ,
,
①当△PBC∽△CAD时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t=10,
故点P的坐标为(﹣1,10),
②当△PBC∽△ACD时, ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t= ![]() ,
,
故点P的坐标为(﹣1, ![]() ),
),
综上所述,点P的坐标为(﹣1,10),(﹣1, ![]() ).
).
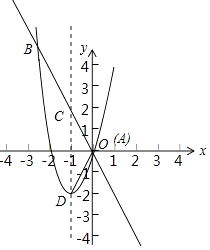
【解析】(1)把抛物线对称轴方程x=﹣1代入直线方程,求得相应的纵坐标,易得点C的坐标;(2)①根据点的坐标的对称性易得抛物线顶点坐标D(﹣1,﹣2),故CD=4,结合三角形的面积公式可以求得点A的坐标,将点A的坐标分别代入抛物线解析式为y=a(x+1)2﹣2,利用待定系数法求得抛物线的解析式即可;②需要分类讨论:△PBD∽△CAD、△PBD∽△ACD.
【考点精析】根据题目的已知条件,利用相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案