题目内容
【题目】某种商品价格为33元/件,某人只带有2元和5元的两种面值的购物劵各若干张,买了一件这种商品;若无需找零钱,则付款方式中张数之和(指付2元和5元购物券的张数)最少和张数之和最多的方式分别是( )
A. 8张和16张 B. 8张和15张 C. 9张和16张 D. 9张和15张
【答案】D
【解析】根据题意可列出一个整式方程,但要分情况讨论结果要符合“只有2元和5元两种面值的人民币”和“无需找零钱”两个条件,注意不要漏解.
解:设付出2元钱的张数为x,付出5元钱的张数为y,且x,y的取值均为自然数,依题意可得方程:
2x+5y=33.则 x=![]() ,
,
解不等式组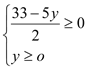 , 解得0≤y≤
, 解得0≤y≤![]() ,
,
又∵y是整数.∴y=0或1或2或3或4或5或6.
又∵x是整数.∴y=1或3或5.
从而此方程的解为:![]() ,
,![]() ,
,
由![]() 得
得![]() ,由
,由![]() 得
得![]() .
.
所以付款方式中张数之和(指付2元和5元购物券的张数)最少和张数之和最多的方式分别是
9张和15张.
“点睛“解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.要注意题解要符合生活常识

练习册系列答案
相关题目