题目内容
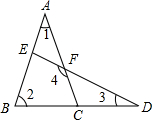
如图，已知∠BOF=120°，则∠A+∠B+∠C+∠D+∠E+∠F=______．
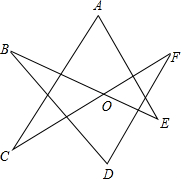
如图，如图，根据三角形的外角性质，∠1=∠A+∠C，∠2=∠B+∠D，
∵∠BOF=120°，
∴∠3=180°-120°=60°，
根据三角形内角和定理，∠E+∠1=180°-60°=120°，
∠F+∠2=180°-60°=120°，
所以，∠1+∠2+∠E+∠F=120°+120°=240°，
即∠A+∠B+∠C+∠D+∠E+∠F=240°．
故答案为：240°．
∵∠BOF=120°，
∴∠3=180°-120°=60°，
根据三角形内角和定理，∠E+∠1=180°-60°=120°，
∠F+∠2=180°-60°=120°，
所以，∠1+∠2+∠E+∠F=120°+120°=240°，
即∠A+∠B+∠C+∠D+∠E+∠F=240°．
故答案为：240°．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
