Question

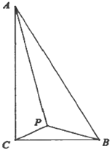
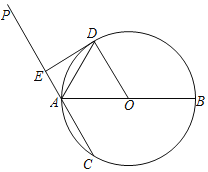
【题目】如图，已知线段，于点，且，是射线上一动点，，分别是，的中点，过点，，的圆与的另一交点（点在线段上），连结，.

（1）当时，求的度数；

（2）求证：；

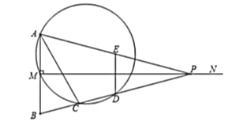
（3）在点的运动过程中，当时，取四边形一边的两端点和线段上一点，若以这三点为顶点的三角形是直角三角形，且为锐角顶点，求所有满足条件的的值.

Answer 1

【答案】（1）75°；（2）证明见解析；（3）或或．

【解析】

（1）根据三角形ABP是等腰三角形，可得∠B的度数；

（2）连接MD，根据MD为△PAB的中位线，可得∠MDB=∠APB，再根据∠BAP=∠ACB，∠BAP=∠B，即可得到∠ACB=∠B，进而得出△ABC∽△PBA，得出答案即可；

（3）记MP与圆的另一个交点为R，根据AM2+MR2=AR2=AC2+CR2，即可得到PR=，MR=，再根据Q为直角三角形锐角顶点，分四种情况进行讨论：当∠ACQ=90°时，当∠QCD=90°时，当∠QDC=90°时，当∠AEQ=90°时，即可求得MQ的值．

解：（1）∵MN⊥AB，AM=BM，

∴PA=PB，

∴∠PAB=∠B，

∵∠APB=30°，

∴∠B=75°，

（2）如图1，连接MD，

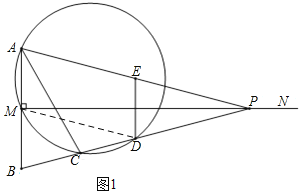
∵MD为△PAB的中位线，

∴MD∥AP，

∴∠MDB=∠APB，

∵∠BAC=∠MDC=∠APB，

又∵∠BAP=180°-∠APB-∠B，∠ACB=180°-∠BAC-∠B，

∴∠BAP=∠ACB，

∵∠BAP=∠B，

∴∠ACB=∠B，

∴AC=AB，由（1）可知PA=PB，

∴△ABC∽△PBA，

∴ ，

∴AB2=BCPB；

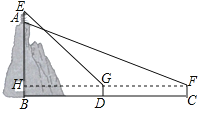
（3）如图2，记MP与圆的另一个交点为R，

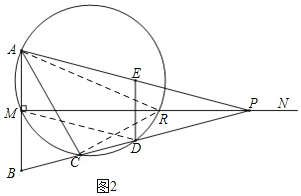
∵MD是Rt△MBP的中线，

∴DM=DP，

∴∠DPM=∠DMP=∠RCD，

∴RC=RP，

∵∠ACR=∠AMR=90°，

∴AM2+MR2=AR2=AC2+CR2，

∴12+MR2=22+PR2，

∴12+（4-PR）2=22+PR2，

∴PR=，

∴MR=，

（一）当∠ACQ=90°时，AQ为圆的直径，

∴Q与R重合，

∴MQ=MR=；

（二）如图3，当∠QCD=90°时，

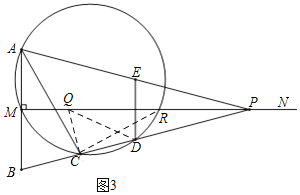
在Rt△QCP中，PQ=2PR=，

∴MQ=；

（三）如图4，当∠QDC=90°时，

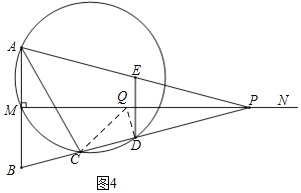
∵BM=1，MP=4，

∴BP=，

∴DP=BP=，

∵cos∠MPB= ，

∴PQ=，

∴MQ=；

（四）如图5，当∠AEQ=90°时，

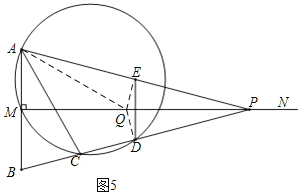
由对称性可得∠AEQ=∠BDQ=90°，

∴MQ=；

综上所述，MQ的值为或或．