题目内容
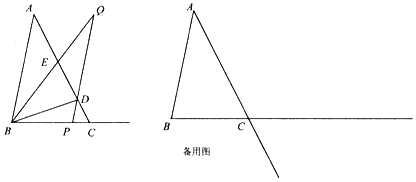
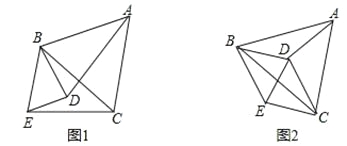
【题目】已知,如图1,△ABC中,BA=BC,D是平面内不与A、B、C重合的任意一点,∠ABC=∠DBE,BD=BE.
(1)求证:△ABD≌△CBE;
(2)如图2,当点D是△ABC的外接圆圆心时,请判断四边形BDCE的形状,并证明你的结论.
【答案】(1)证明见解析(2)四边形BDEF是菱形,证明见解析
【解析】
(1)证明:∵∠ABC=∠DBE,∴∠ABC+∠CBD=∠DBE+∠CBD。∴∠ABD=∠CBE。
在△ABD与△CBE中,BA=BC,∠ABD=∠CBE,BD=BE,
∴△ABD≌△CBE(SAS) 。
(2)解:四边形BDEF是菱形。证明如下:
由(1)△ABD≌△CBE,∴CE=AD。
∵点D是△ABC外接圆圆心,∴DA=DB=DC。
又∵BD=BE,∴BD=BE=CE=CD。
∴四边形BDCE是菱形。
(1)由∠ABC=∠DBE,根据等量加等量和相等,得∠ABD=∠CBE,从而根据SAS即可证得结论。
(2)由三角形外接圆圆心到三个顶点距离相等的性质和(1)的结论,得到四边形四边相等,从而得出结论。

练习册系列答案
相关题目