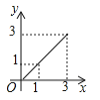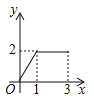题目内容
【题目】二次函数y=ax2+bx+c (a≠0)的图象如图所示,对称轴是x=-1.下列结论:①ab>0;②b2>4ac;③a-b+2c<0;④8a+c<0.其中正确的是( )

A. ③④ B. ①②③ C. ①②④ D. ①②③④
【答案】C
【解析】分析: 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断即可.
详解: ①对称轴在y轴的左侧,a,b同号,
∴ab>0,
故①正确;
②由图知:抛物线与x轴有两个不同的交点,
则△=b4ac>0,
∴b2>4ac,
故②正确;
③∵x=-1时,y>0,
∴a-b+c>0,
而c>0,
∴a-b+2c>0,所以④错误;
④由图知:当x=2时y<0,所以4a+2b+c<0,因为b=2a,所以4a+4a+c<0,即8a+c<0,故⑤正确;
故选:C.
点睛: 本题考查的是二次函数图象与系数的关系,掌握二次函数y=ax2+bx+c系数符号与抛物线开口方向、对称轴、抛物线与y轴的交点、抛物线与x轴交点的个数的关系是解题的关键.

【题目】喜迎新年,某社区超市第一次用5000元购进甲、乙两种商品,其中甲商品件数是品的件数的2倍,甲、乙两种商品的进价和售价如下表:
甲 | 乙 | |
进价(元/件) | 15 | 20 |
售价(元/件) | 30 | 30 |
(1)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(2)能市第二次以第一次的进价又购进甲、乙两种商品,其中购进乙种商品的件数不变,购进甲种商品的件数是第一次购进甲种商品件数的2倍;乙商品按原价销售,甲商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多600元,求第二次甲种商品按原价打几折销售?
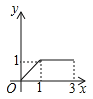
【题目】在大课间活动中,体育老师随机抽取了七年级甲、乙两班部分女学生进行仰卧起坐的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分 组 | 频数 | 频率 |
第一组(0≤x<15) | 3 | 0.15 |
第二组(15≤x<30) | 6 | a |
第三组(30≤x<45) | 7 | 0.35 |
第四组(45≤x<60) | b | 0.20 |
(1)频数分布表中a=_____,b=_____,并将统计图补充完整;
(2)如果该校七年级共有女生180人,估计仰卧起坐能够一分钟完成30或30次以上的女学生有多少人?
(3)已知第一组中只有一个甲班学生,第四组中只有一个乙班学生,老师随机从这两个组中各选一名学生谈心得体会,则所选两人正好都是甲班学生的概率是多少?