题目内容
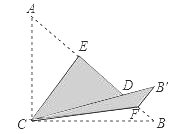
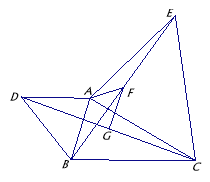
【题目】如图,已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE.G、F分别是DC与BE的中点.
(1)求证:DC=BE;
(2)当∠DAB=80°,求∠AFG的度数;
(3)若∠DAB=![]() ,则∠AFG与
,则∠AFG与![]() 的数量关系是 .
的数量关系是 .
【答案】(1)证明见解析;(2)50°;(3)∠AFG= 90°-![]() .
.
【解析】
试题(1)由∠DAB=∠CAE知∠DAC=∠BAE,又DA=AB,AE=AC,所以△ADC≌△ABE,由此可得:DC=BE;
(2)易证△ADC≌△ABE可得CG=EF;又AE=AC,∠AEF=∠ACG,EF=CG,所以△AEF≌△AGC.可得AF=AG,且∠EAF=∠CAG,所以∠AFG=∠AGF,∠FAG=∠EAC=80°从而可求∠AFG=![]() (180°-80°)=50°.
(180°-80°)=50°.
(3)由(2)知:∠AFG=90°-![]() .
.
试题解析:(1)∵∠DAB=∠CAE∠D
∴AC=∠BAE,
又DA=AB,AE=AC,
所以△ADC≌△ABE
∴DC=BE;
(2)当∠DAB=80°.∵∠DAB=∠CAE,
∴∠DAB+∠BAC=∠CAE+∠BAC,
即∠DAC=∠BAE,
在△ADC与△ABE中,
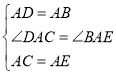
∴△ADC≌△ABE ,
∴DC=BE,∠AEF=∠ACG,
∵G、F分别是DC与BE的中点,
∴CG=EF;
连AG,在△AEF与△AGC中,
∵AE=AC,∠AEF=∠ACG,EF=CG
∴△AEF≌△AGC,
∴AF=AG,且∠EAF=∠CAG,
∴∠AFG=∠AGF,∠FAG=∠EAC=80°,
∴∠AFG=![]() (180°-80°)=50°.
(180°-80°)=50°.
(3)∠AFG=90°-![]() .
.
考点: 全等三角形的判定与性质.

练习册系列答案
相关题目