题目内容
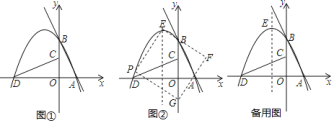
【题目】已知，直线y=2x+3与直线y=﹣2x﹣1.
（1）求两直线与y轴交点A，B的坐标；
（2）求两直线交点C的坐标；
（3）求△ABC的面积．
【答案】（1）A（0，3），B（0，-1）；
（2）点C的坐标为（-1，1）；
（3）S△ABC= 2.
【解析】
（1）利用待定系数法即可解决问题；
（2）构建方程组确定交点坐标即可；
（3）过点C作CD⊥AB交y轴于点D，根据S△ABC=
ABCD计算即可.
（1）在y=2x+3中，当x=0时，y=3，即A（0，3）；
在y=-2x-1中，当x=0时，y=-1，即B（0，-1）；
（2）依题意，得
，
解得
；
∴点C的坐标为（-1，1）；
（3）过点C作CD⊥AB交y轴于点D；
∴CD=1；
∵AB=3-（-1）=4；
∴S△ABC=ABCD=×4×1=2.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某农产品生产基地收获红薯192吨，准备运给甲、乙两地的承包商进行包销．该基地用大、小两种货车共18辆恰好能一次性运完这批红薯，已知这两种货车的载重量分别为14吨/吨和8吨/辆，运往甲、乙两地的运费如下表：
车型 | 运费 | |
运往甲地/（元/辆） | 运往乙地/（元/辆） | |
大货车 | 720 | 800 |
小货车 | 500 | 650 |
（1）求这两种货车各用多少辆；
（2）如果安排10辆货车前往甲地，其余货车前往乙地，其中前往甲地的大货车为a辆，总运费为w元，求w关于a的函数关系式；
（2）在（2）的条件下，若甲地的承包商包销的红薯不少于96吨，请你设计出使总运费最低的货车调配方案，并求出最低总运费．
