题目内容
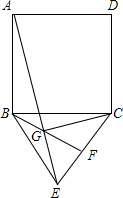如图正方形ABCD的面积为64，三角形BCE是等边三角形，F是CE的中点，AE，BF交于点G，连接CG，则CG=________．
4
分析：根据等边三角形的性质和正方形的性质得到AB=BE，进而得到∠BFA=15°，然后利用垂直平分线的性质判定△GFC为等腰直角三角形，从而求出线段GC的长．
解答：∵△BCE是等边三角形，四边形ABCD为正方形，
∴BA=BE，
∵∠ABE=∠ABC+∠CBE=90°+60°=150°，
∴∠BEA=∠BAE=15°，
∴∠AEC=60°-15°=45°，
∵正方形ABCD的面积为64，
∴EC=BC=8，
∵F是CE的中点，
∴BF⊥FC，FC=4，
∴△GFC为等腰直角三角形，
∴GC=4．
故答案为4．
点评：本题考查了正方形、等边三角形的性质及垂直平分线的性质，解决本题的关键是判定△GFC为等腰直角三角形．
分析：根据等边三角形的性质和正方形的性质得到AB=BE，进而得到∠BFA=15°，然后利用垂直平分线的性质判定△GFC为等腰直角三角形，从而求出线段GC的长．
解答：∵△BCE是等边三角形，四边形ABCD为正方形，
∴BA=BE，
∵∠ABE=∠ABC+∠CBE=90°+60°=150°，
∴∠BEA=∠BAE=15°，
∴∠AEC=60°-15°=45°，
∵正方形ABCD的面积为64，
∴EC=BC=8，
∵F是CE的中点，
∴BF⊥FC，FC=4，
∴△GFC为等腰直角三角形，
∴GC=4
．故答案为4
．点评：本题考查了正方形、等边三角形的性质及垂直平分线的性质，解决本题的关键是判定△GFC为等腰直角三角形．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
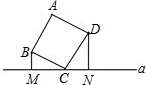如图正方形ABCD的顶点C在直线a上，且点B，D到a的距离分别是1，2．则这个正方形的边长为（ ）| A、1 | ||
| B、2 | ||
| C、4 | ||
D、
|
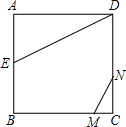如图正方形ABCD的边长为2，AE=EB，线段MN的两端点分别在CB、CD上滑动，且MN=1，当CM为何值时△AED与以M、N、C为顶点的三角形相似？
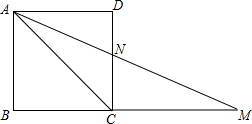如图正方形ABCD的边BC的延长线上取点M，使CM=AC=2，AM与CD相交于点N，∠ANC=
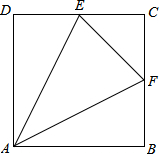（2013•鄂州）如图正方形ABCD的边长为4，E、F分别为DC、BC中点．
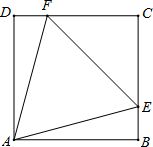如图正方形ABCD的边长是a，△AEF是等边三角形，点E在BC上，点F在CD上