题目内容
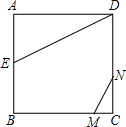 如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似?
如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似?
分析:根据AE=EB,△AED中AD=2AE,所以在△MNC中,分CM与AE和AD是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系,然后利用勾股定理列式计算即可.
解答:解:∵AE=EB,∴AD=2AE,
又∵△AED与以M、N、C为顶点的三角形相似,
∴(1)CM与AD是对应边时,CM=2CN,
∴CM2+CN2=MN2=1,
即CM2+
CM2=1,
解得CM=
;
(2)CM与AE是对应边时,CM=
CN,
∴CM2+CN2=MN2=1,
即CM2+4CM2=1,
解得CM=
.
所以CM为
或
时,△AED与以M、N、C为顶点的三角形相似.
又∵△AED与以M、N、C为顶点的三角形相似,
∴(1)CM与AD是对应边时,CM=2CN,
∴CM2+CN2=MN2=1,
即CM2+
| 1 |
| 4 |
解得CM=
2
| ||
| 5 |
(2)CM与AE是对应边时,CM=
| 1 |
| 2 |
∴CM2+CN2=MN2=1,
即CM2+4CM2=1,
解得CM=
| ||
| 5 |
所以CM为
2
| ||
| 5 |
| ||
| 5 |
点评:本题主要利用相似三角形对应边成比例的性质和直角三角形勾股定理求解.

练习册系列答案
 智慧课堂密卷100分单元过关检测系列答案
智慧课堂密卷100分单元过关检测系列答案
相关题目
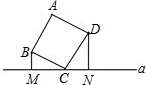 如图正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长为( )
如图正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长为( )| A、1 | ||
| B、2 | ||
| C、4 | ||
D、
|
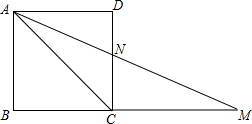 如图正方形ABCD的边BC的延长线上取点M,使CM=AC=2,AM与CD相交于点N,∠ANC=
如图正方形ABCD的边BC的延长线上取点M,使CM=AC=2,AM与CD相交于点N,∠ANC=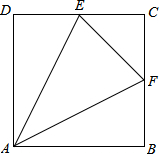 (2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点.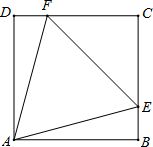 如图正方形ABCD的边长是a,△AEF是等边三角形,点E在BC上,点F在CD上
如图正方形ABCD的边长是a,△AEF是等边三角形,点E在BC上,点F在CD上