题目内容
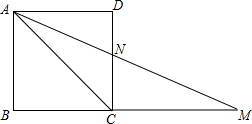 如图正方形ABCD的边BC的延长线上取点M,使CM=AC=2,AM与CD相交于点N,∠ANC=
如图正方形ABCD的边BC的延长线上取点M,使CM=AC=2,AM与CD相交于点N,∠ANC=分析:作辅助线,过点C作CE⊥AM交AM于点E,
(1)AC为正方形ABCD的对角线,可知:∠ACB=45°,根据CA=CM,可知∠MCE的度数,进而可知∠ECN的度数,故∠ANC=∠ECN+∠CEN;
(2)根据CA,CM的长和∠ACM的度数,代入S=
CA×CM×sin∠ACM,计算即可.
(1)AC为正方形ABCD的对角线,可知:∠ACB=45°,根据CA=CM,可知∠MCE的度数,进而可知∠ECN的度数,故∠ANC=∠ECN+∠CEN;
(2)根据CA,CM的长和∠ACM的度数,代入S=
| 1 |
| 2 |
解答: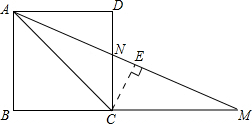 解:过点C作CE⊥AM交AM于点E
解:过点C作CE⊥AM交AM于点E
(1)∵AC为正方形ABCD的对角线,
∴∠ACB=45°,
∴∠MCE=∠ACE=
(180°-45°)=67.5°,
∠ECN=90°-∠MCE=22.5°,
∵∠CEN=90°,
∴∠ANC=22.5°+90°=112.5°.
(2)∵AC=AM=2,∠ACM=135°,
∴S△ACM=
CA×CM×sin∠ACM=
×2×2×
=
.
 解:过点C作CE⊥AM交AM于点E
解:过点C作CE⊥AM交AM于点E(1)∵AC为正方形ABCD的对角线,
∴∠ACB=45°,
∴∠MCE=∠ACE=
| 1 |
| 2 |
∠ECN=90°-∠MCE=22.5°,
∵∠CEN=90°,
∴∠ANC=22.5°+90°=112.5°.
(2)∵AC=AM=2,∠ACM=135°,
∴S△ACM=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| 2 |
点评:本题应注意三角形面积的多种求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
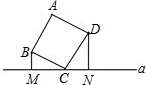 如图正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长为( )
如图正方形ABCD的顶点C在直线a上,且点B,D到a的距离分别是1,2.则这个正方形的边长为( )| A、1 | ||
| B、2 | ||
| C、4 | ||
D、
|
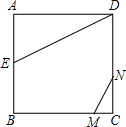 如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似?
如图正方形ABCD的边长为2,AE=EB,线段MN的两端点分别在CB、CD上滑动,且MN=1,当CM为何值时△AED与以M、N、C为顶点的三角形相似?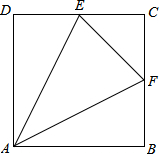 (2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点.
(2013•鄂州)如图正方形ABCD的边长为4,E、F分别为DC、BC中点.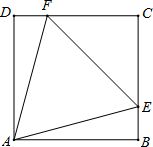 如图正方形ABCD的边长是a,△AEF是等边三角形,点E在BC上,点F在CD上
如图正方形ABCD的边长是a,△AEF是等边三角形,点E在BC上,点F在CD上