题目内容
【题目】△ABC中，AB=15，AC=20，BC边上的高AD=12，则BC的长为（ ）
A.25B.7C.25或7D.14或4
【答案】C
【解析】
已知三角形两边的长和第三边的高，未明确这个三角形为钝角还是锐角三角形，所以需分类讨论，即∠ABC是钝角还是锐角，然后利用勾股定理求解．
（1）如图1，△ABC中，AB=15，AC=20，BC边上高AD=12，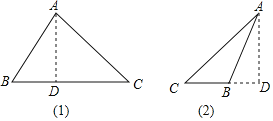
在Rt△ABD中：AB=15，AD=12，由勾股定理得
，
在Rt△ADC中AC=20，AD=12，由勾股定理得
，
∴BC的长为：
．
如图2，△ABC中，AB=15，AC=20，BC边上高AD=12，
在Rt△ABD中AB=15，AD=12，由勾股定理得，
在Rt△ACD中AC=20，AD=12，由勾股定理得，
∴BC的长为：
．
综上所述，BC的长为：25或7．
故选：C．
练习册系列答案
科学实验活动册系列答案
相关题目
