��Ŀ����
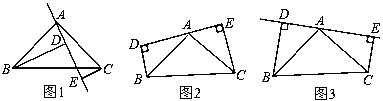
����Ŀ��ͼ1�������ɸ�СԲȦ�ѳɵ�һ������ȱ������ε�ͼ����������һ����һ��ԲȦ�����¸��������һ���һ��ԲȦ��һ������![]() ����
����
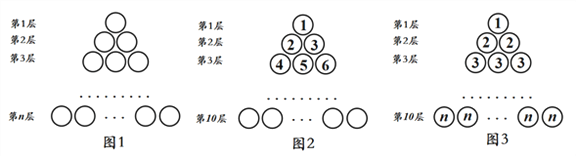
��1�����ú���![]() ��ʽ�ӱ�ʾ��ͼ1������ԲȦ�ĸ�����
��ʽ�ӱ�ʾ��ͼ1������ԲȦ�ĸ�����
��2�����ͼ1�е�ԲȦ����10��������������������ÿ��ԲȦ�ж���ͼ2�ķ�ʽ����һ��������������1��2��3��4![]()
![]() ������ײ����ұ����ԲȦ�е������� ��
������ײ����ұ����ԲȦ�е������� ��
��3������������������ÿ��ԲȦ�ж���ͼ3�ķ�ʽ����һ��������������1��2��2��3��3��3�����������ͼ3������ԲȦ�и���֮����
���𰸡���1��![]() ����2��55����3��385��
����2��55����3��385��
�������������������1������ͼ����ԲȦ�ĸ����仯���ɵó��𰸼��ɣ�
��2����10����10���������ұ�һ����Ϊ��1+2+3+��+10��
��3���������ֺ�Ϊ��1+2��2+3��3+4��4+��+10��10��
����������⣺��1��ͼ1������ԲȦ�ĸ���Ϊ�� ![]() ����
����
��2����10����10���������ұ�һ����Ϊ��1+2+3+��+10=55 ��
��3��ͼ3������ԲȦ�и���֮�ͣ�
1+2��2+3��3+4��4+��+10��10=![]() =
=![]() =385��
=385��

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ