题目内容
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC,AE是过A的一条直线,且B,C在AE的异侧,BD⊥AE于点D,CE⊥AE于点E.
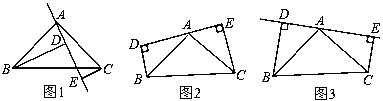
(1)求证:BD=DE+CE;
(2)若直线AE绕点A旋转到图2位置时(BD<CE),其余条件不变,问BD与DE,CE的关系如何,请证明;
(3)若直线AE绕点A旋转到图3时(BD>CE),其余条件不变,BD与DE,CE的关系怎样?请直接写出结果,不须证明.
【答案】(1)证明见解析;(2)BD=DE+CE;(3)BD=DE+CE.
【解析】
试题分析:本题考查了全等三角形的判定和性质,涉及到直角三角形的性质、余角和补角的性质等知识点,熟练掌握全等三角形的判定方法是解题的关键.
(1)根据已知条件易证得∠BAD=∠ACE,且根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(2)BD=DE+CE.根据全等三角形的判定可证明△ABD≌△CAE,根据各线段的关系即可得结论.
(3)同上理,BD=DE+CE仍成立.
试题解析:(1)在△ABD和△CAE中,
∵∠CAD+∠BAD=90°,∠BAD+∠ABD=90°,∴∠CAD=∠ABD.
又∠ADB=∠AEC=90°,AB=AC,∴△ABD≌△CAE.(AAS),
∴BD=AE,AD=CE.又AE=AD+DE,∴AE=DE+CE,即BD=DE+CE.
(2)BD=DE﹣CE.
∵∠BAC=90°,∴∠BAD+∠CAE=90°.又∵BD⊥DE,∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.又AB=AC,∠ADB=∠CEA=90°,∴△ADB≌△CEA.∴BD=AE,AD=CE.
∵DE=AD+AE,
∴DE=CE+BD,即 BD=DE﹣CE
(3)同理:BD=DE﹣CE.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
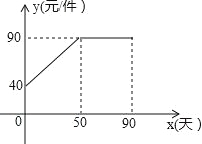
小学生10分钟应用题系列答案【题目】九年级(3)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售量的相关信息如下.已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为w(单位:元).
时间x(天) | 1 | 30 | 60 | 90 |
每天销售量p(件) | 198 | 140 | 80 | 20 |
(1)求出w与x的函数关系式;
(2)问销售该商品第几天时,当天的销售利润最大?并求出最大利润;
(3)该商品在销售过程中,共有多少天每天的销售利润不低于5600元?请直接写出结果.