题目内容
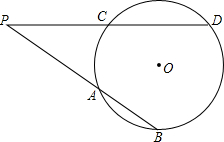 如图,P是圆O外的一点,点B、D在圆上,PB、PD分别交圆O于点A、C,如果AP=4,AB=2,PC=CD,那么PD=
如图,P是圆O外的一点,点B、D在圆上,PB、PD分别交圆O于点A、C,如果AP=4,AB=2,PC=CD,那么PD=考点:切割线定理
专题:几何图形问题
分析:根据“从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等”得到:PA•PB=PC•PD,即PA•PB=
PD2.
| 1 |
| 2 |
解答:解:如图,∵AP=4,AB=2,PC=CD,
∴PB=AP+AB=6,PC=
PD.
又∵PA•PB=PC•PD,
∴4×6=
PD2,
则PD=4
.
故答案是:4
.
∴PB=AP+AB=6,PC=
| 1 |
| 2 |
又∵PA•PB=PC•PD,
∴4×6=
| 1 |
| 2 |
则PD=4
| 3 |
故答案是:4
| 3 |
点评:本题考查了切割线定理.
(1)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
(2)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.
(1)切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项.
(2)推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.

练习册系列答案
相关题目
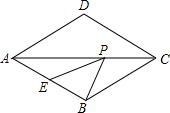 如图,点P是菱形ABCD对角线AC上一动点,点E是AB的中点,若AD=2,∠DAB=60°,则PB+PE的最小值是( )
如图,点P是菱形ABCD对角线AC上一动点,点E是AB的中点,若AD=2,∠DAB=60°,则PB+PE的最小值是( )