题目内容
已知a+b+c=0，试求
+
+
的值．
| a2 |
| 2a2+bc |
| b2 |
| 2b2+ac |
| c2 |
| 2c2+ab |
考点：分式的化简求值
专题：计算题
分析：由a+b+c=0，得到c=-a-b，代入原式中计算即可得到结果．
解答：解：∵a+b+c=0，即c=-a-b，
∴原式=
+
+
=
+
=
+
=
+
=
=1．
∴原式=
| a2 |
| 2a2-b(a+b) |
| b2 |
| 2b2-a(a+b) |
| (a+b)2 |
| 2(a+b)2+ab |
=
| 2a2b+a3-2ab2-b3 |
| (a-b)(2a+b)(2b+a) |
| a2+b2+2ab |
| 2a2+2b2+5ab |
=
| (a-b)(2ab+a2+b2+ab) |
| (a-b)(2a+b)(2b+a) |
| a2+b2+2ab |
| 2a2+2b2+5ab |
=
| 2ab+a2+b2+ab |
| (2a+b)(2b+a) |
| a2+b2+2ab |
| (2a+b)(2b+a) |
=
| 2a2+2b2+5ab |
| 2a2+2b2+5ab |
=1．
点评：此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
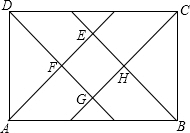如图，在矩形ABCD中，AE、BE、CG、DG分别是各内角的平分线，E、F、G、H分别为它们的交点．求证：四边形EFGH是正方形．
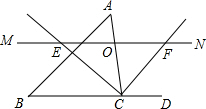如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
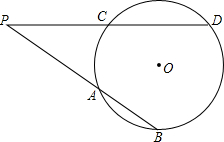如图，P是圆O外的一点，点B、D在圆上，PB、PD分别交圆O于点A、C，如果AP=4，AB=2，PC=CD，那么PD=