题目内容
已知在直角ABC中，∠C=90°，AC=8，BC=6，则△ABC的外接圆半径长为 ．
考点：三角形的外接圆与外心
专题：计算题
分析：根据勾股定理求出斜边，根据直角三角形的外接圆的半径等于斜边的一半求出即可．
解答：解：由勾股定理得：AB=
=
=10，
∵△ACB是直角三角形，
∴△ABC的外接圆半径长为斜边的一半，即是5，
故答案为：5．
| AC2+BC2 |
| 82+62 |
∵△ACB是直角三角形，
∴△ABC的外接圆半径长为斜边的一半，即是5，
故答案为：5．
点评：本题考查了勾股定理和直角三角形的外接圆的应用，注意：直角三角形的外接圆的半径等于斜边的一半．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
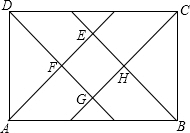如图，在矩形ABCD中，AE、BE、CG、DG分别是各内角的平分线，E、F、G、H分别为它们的交点．求证：四边形EFGH是正方形．
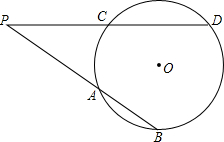如图，P是圆O外的一点，点B、D在圆上，PB、PD分别交圆O于点A、C，如果AP=4，AB=2，PC=CD，那么PD=下列角度中，不能成为多边形内角和的是（ ）
| A、540° | B、800° |
| C、900° | D、1800° |