题目内容
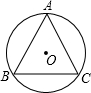
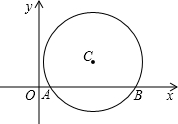
如图,⊙O是△ABC的外接圆,且AB=AC=13,BC=24,求⊙O的半径.
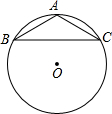

连接OA交BC于点D,连接OC,OB,
∵AB=AC=13,
∴
=
,
∴∠AOB=∠AOC,
∵OB=OC,
∴AO⊥BC,CD=
BC=12
在Rt△ACD中,AC=13,CD=12
所以AD=
=5
设⊙O的半径为r
则在Rt△OCD中,OD=r-5,CD=12,OC=r
所以(r-5)2+122=r2
解得r=16.9.
答:⊙O的半径为16.9.
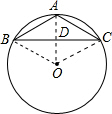
∵AB=AC=13,
∴
 |
| AB |
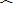 |
| AC |
∴∠AOB=∠AOC,
∵OB=OC,
∴AO⊥BC,CD=
| 1 |
| 2 |
在Rt△ACD中,AC=13,CD=12
所以AD=
| 132-122 |
设⊙O的半径为r
则在Rt△OCD中,OD=r-5,CD=12,OC=r
所以(r-5)2+122=r2
解得r=16.9.
答:⊙O的半径为16.9.


练习册系列答案
相关题目
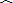

 -4,0)、(2,0).
-4,0)、(2,0).