题目内容
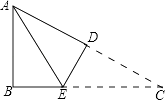
【题目】如图,已知四边形ABCD中,对角线BD平分∠ABC,∠ACB=72°,∠ABC=50°,并且∠BAD+∠CAD=180°,那么∠ADC的度数为( ) 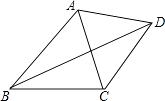
A.62°
B.65°
C.68°
D.70°
【答案】B
【解析】 解:延长BA和BC,过D点作DE⊥BA于E点,过D点作DF⊥BC于F点,
∵BD是∠ABC的平分线
在△BDE与△BDF中,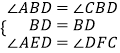 ,
,
∴△BDE≌△BDF,
∴DE=DF,
又∵∠BAD+∠CAD=180°,
∠BAD+∠EAD=180°,
∴∠CAD=∠EAD,
∴AD为∠EAC的平分线,
过D点作DG⊥AC于G点,
在RT△CDG与RT△CDF中,![]() ,
,
∴RT△ADE≌RT△ADG,
∴DE=DG,
∴DG=DF.
在RT△CDG与RT△CDF中,![]() ,
,
∴RT△CDG≌RT△CDF,
∴CD为∠ACF的平分线
∠ACB=72°
∴∠DCA=54°,
△ABC中,
∵∠ACB=72°,∠ABC=50°,
∴∠BAC=180°﹣72°﹣50°=58°,
∴∠DAC= ![]() =61°,
=61°,
∴∠ADC=180°﹣∠DAC﹣∠DCA=180°﹣61°﹣54°=65°.
故选:B.
【考点精析】本题主要考查了多边形内角与外角的相关知识点,需要掌握多边形的内角和定理:n边形的内角和等于(n-2)180°.多边形的外角和定理:任意多边形的外角和等于360°才能正确解答此题.

练习册系列答案
相关题目