题目内容
【题目】如图,AD∥BC,∠EAD=∠C,∠FEC=∠BAE,∠EFC=50°
(1)求证:AE∥CD;
(2)求∠B的度数. 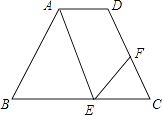
【答案】
(1)证明:∵AD∥BC,
∴∠D+∠C=180°,
∵∠EAD=∠C,
∴∠EAD+∠D=180°,
∴AE∥CD;
(2)∵AE∥CD,
∴∠AEB=∠C,
∵∠FEC=∠BAE,
∴∠B=∠EFC=50°.
【解析】(1)根据平行线的性质和等量关系可得∠EAD+∠D=180°,根据同旁内角互补,两直线平行即可证明;(2)根据平行线的性质可得∠AEB=∠C,根据三角形内角和定理和等量关系即可得到∠B的度数.
【考点精析】关于本题考查的平行线的判定,需要了解同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行才能得出正确答案.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目