Question

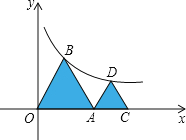
【题目】如图，矩形ABCD中，AB=1，BC=2，BC在x轴上，一次函数y=kx﹣2的图象经过点A、C，并与y轴交于点E，反比例函数y=的图象经过点A．

（1）点E的坐标是 ；

（2）求反比例函数的解析式；

（3）求当一次函数的值小于反比例函数的值时，x的取值范围．

Answer 1

【答案】（1）E（0，﹣2）；（2）y=（3）x＜﹣2或 0＜x＜6

【解析】

试题分析：（1）一次函数y=kx﹣2中代入x=0求得y的值，即可求得点E的坐标；

（2）利用△ACD∽△CEO求得点A的坐标后代入反比例函数的解析式，即可求得反比例函数的解析式；

（3）首先确定两个函数的交点坐标，然后结合图象确定x的取值范围即可．

解：（1）一次函数y=kx﹣2中令x=0得y=﹣2，

所以E（0，﹣2）；

（2）∵∠OCE=∠ACB，

∴Rt△OCE∽Rt△BCA，

∴=，

即=，

解得OC=4，

∴C点坐标为（4，0）；

（2）把C（4，0）代入y=kx﹣2得4k﹣2=0，解得k=，

∴一次函数解析式为y=x﹣2；

∵OC=4，

∴A点坐标为（6，1），

把A（6，1）代入y=得m=6×1=6，

∴反比例函数解析式为y=；

（3）令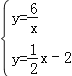

解得，

∴另一个交点（﹣2，﹣3），

∴观察图象得：当x＜﹣2或 0＜x＜6时次函数的值小于反比例函数的值．